在《以数织图》里，玩家可以挑战各种各样的数字关卡。每一关都需要通过填充格子来完成挑战，随着关卡难度的提升，给出的提示也会变得越来越复杂，玩家得动动脑筋才能成功解开格子里隐藏的图形。游戏中还为玩家准备了丰富的提示功能，玩家可以借助这些提示找到解题思路，从而顺利通过关卡。

游戏背景：

以数织图包含丰富的关卡内容，玩家需通过填格操作来绘制图形。游戏内设置了多个关卡，每个关卡的填格顺序均有差异，玩家要依据两侧的数字提示确定填格顺序，从而成功完成关卡图像的绘制。

游戏特色

1、无论是数字类还是文字类的纵横游戏都十分好用，你对它们很熟悉，其玩法也极具吸引力，让人容易沉浸其中。

2、这里有多种主题的拼图可供您挑战，记得领取完成后的成就奖励哦

3、5种挑战模式，选择最适合您的数织游戏难度等级

4、轻松愉快的背景音乐，能使自己快速放松下来

以数织图游戏攻略

本系列中的简称及其说明

1、排：行/列

2、垂直：与排的方向垂直。

3、从k排起始的m×n区块：未明确指出具体范围时，一般指代游戏里所有排的整体集合；此外，它也可用来表示一个矩形区域，这里的m代表行数，n代表列数。

4、场地格：初始状态的格子，存在在游戏的区块中。

5、第x行格：从任意一边开始数的第x个场地格

6、第x个数字：从任意一边开始数第x个数字

7、数字x的正格：是指必定存在黑块的格子，并且这个场地格肯定是数字x的图形的组成部分

8、负格：一定无黑块的格子

9、数字x的位：数字x所可能代表的场地格

第一章：数字的位与数字的位的确定化

1-1概述

在数织时，我们需要处理那些位置模糊的区域，借助这些区域和各个区块之间的关联，就能把其中一部分的精确位置确定下来，最终顺利推导出完整的图像。

数字的准确位置通常能通过一排的格数和数字推导得出，偶尔也需借助已确定的正格与负格，仅有极少数关卡需要同时运用两排以上的信息。这也让它的难度不会太高，本系列旨在帮助您从刚入门的新手快速成长为能推理大多数图形的高手。

注：以下所有定理与方法中我们将把负数看为零。

1-2 推演基础

怎样才能借助推演来确定精准的位置呢？我们不妨先提出一条极为简单的定理。

若某一排中存在且仅存在一个数字，那么该排中所有非数字所在位置的场地格都属于负格。(1-2-1)

这条定理无需证明即可成立，也可以看作是数字位定义的另一种表述方式。

从这条公理中我们能够发现，要确定一个数字的精确位置，关键在于把它的位数缩减到不能再缩减的程度。而交叉排列与单一排列的限制条件，能够助力我们实现数字位数的减少。

我们来看一个简单的例子。

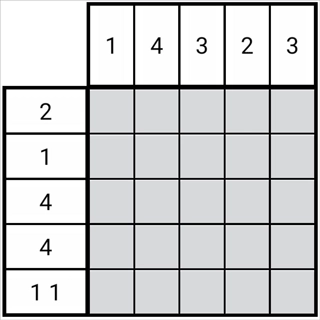
图1-2-1

如图所示，每一排的黑块在既定规则下仅存在有限种分布情形，这些分布情形被称作分布可能。

图中第二列存在两种分布情况，这两种情况之间有部分重叠区域，从图中能发现，该重叠区域里的格子必然是正格。

同理，图中第三列存在三种可能的分布情况，而这三种分布情况同样存在公共区域——第三列第三格。因此，这个格子也必然是正格。

更普遍地说，在一排的所有可能分布里，始终存在黑块的格子被称为正格。

如果一个排里存在一个正格，并且这个正格里只有一个数字，我们可以把它当作“固定”住该数字所在位置的“钉子”，而位置能够在它的左右两侧“变动”，或者说增加格的数量，以此推导出所有可能的分布情况。

同时，若有两个正格将某个数字的位置固定住，那么它们之间的部分也必然确定为正格。我们同样可以用数学语言将这一规律转化为如下表述：

若某一排中只有一个数字，并且已知第m行的格子和第n行的格子都是正格，那么第i行的格子也为正格。这里的i是满足m≤x≤n或n≤x≤m的正整数x。(1-2-2)

然而，由于数字的大小关联，一个数字的位会在正格的两侧增加特定数量的格数。这一增加不能超出数字所限定的范围，因此我们从数学层面展开推导。

假设某一排中恰好存在一个数字k，已知第m行格和第n行格均为正格，且m≥n。根据式1-2-2可以推断，这两个正格之间的所有格子也都是正格，这些正格的总数为(m - n + 1)个。由此可知，该数字k在这一排中还能在左右两侧增加的格子数量为k - (m - n + 1)。因此，只需从已有的正格区域两端各增加相应数量的格子，就能得到该数字k所有的占位。也就是说，从第n - [k - (m - n + 1)]行格到第m + [k - (m - n + 1)]行格都属于数字k的占位范围。经过整理后可得出：

若某一排中存在且仅存在一个数字k，同时第m行格与第n行格均为正格（其中m≧n），则该数字的位置范围是从第(-k+m+1)行格至第(k+n-1)行格。(1-2-2)

1-3边缘法

我们之前提到，数字可以对“位”形成限制，实际上，还有一样事物也能起到这种限制作用——那就是场地格的边缘。场地格边缘之外显然不可能存在“位”，特别是第一个数字，它往往离场地格的边缘最近，因此很容易被边缘所限制。基于此，我们有必要针对边缘的情况展开讨论。

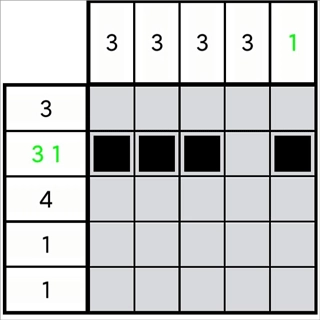
图1-3-1

如图1-3-1所示，很明显图中第1列的位无法向上增加两格，但它确实符合定理(1-2-3)的前置条件。我们可以换个思路：既然不能向上增加，那就必须向下增加。所以，向上不能增加的格数，需要通过向下增加相同的格数来补足。

设一排中存在且仅存在一个数字m，同时已知第n行的格子为正格，并且满足m＞n的条件。那么，这一排中无法再增加的格子数量为(m - n)格。若将这些无法增加的格子数量沿着向下的方向进行增加操作，就能够得到：

当某一排中存在且仅存在一个数字m，同时第n行的格子为正格，且满足m大于n时，那么对于所有属于正整数集合且处于[n，m]区间内的i值，第i行的格子均为正格。(1-3-1)

观察这个定理，当m＞n时，意味着该数字对应的位必然覆盖了从第1行格到第n行格的范围。若我们将其假定为第一个数字，不难发现这个定理仍然是成立的。由此可得：

若某一排中第n行的格为正格，且该正格的第一个数字是m（m>n），那么对于满足i∈[n，m]且i为正整数的所有i，第i行的格均为正格。(1-3-2)

当某个数字处于边缘位置时，它的状态不会有太大改变，不过，要是我们探讨一整排的情形，那又会是怎样的呢？

这里我们介绍一种思路：整体法。在确定两个相邻数字的位时，我们可以把这两个数字当作一个整体来处理，它们各自的位也相应地视为这个整体的位。这种处理方式不仅能简化运算过程，还有助于我们对一整排数字的情况进行分析。

我们可以留意到这样一个事实：当由多个数字构成的整体位于边缘位置时，会呈现出一种独特的分布形式——数字-空格-数字-空格。这种分布方式能将数字所占据的空间压缩到最小，我们把这种整体处于边缘时的分布状态称作边缘状态。

当一个实心物体在直道中滑动时，不难想象，它的投影与初始投影的公共部分会持续缩小。所以，该物体所有运动瞬间投影的公共部分，其实和它处于边缘状态时投影的公共部分是一样的。据此，我们能够得出：

没有负格的一排中所有可能分布的公共部分由其边缘状态决定。

可以看出，这种描述乍看之下十分完美，实际上存在一点瑕疵——作为一个整体，多个数字所占据的空间能够拉长或缩短，而边缘状态必然是最短的。不过确实，我们距离完善它仅差一步之遥。

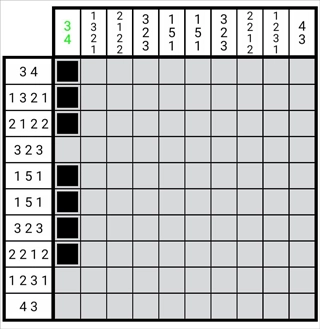
图1-3-2

如图所示，我们能够在第一列自上而下构建一个图形，该图形呈现的是第一列所有数字整体的边缘状态。此时，这一列从下往上数总共有2个空格，这表明该图形里每个数字的位都能向下延伸两格。因此，我们按照图示，将图形中与每个数字对应的图形从上到下减去两格。

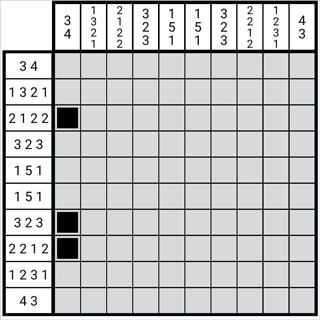
图1-3-3

通过这种方式，我们便得到了该列的正格。采用这种方法最终生成的图形，和原始图形的数字位是相互对应的。此处我们没有对边缘状态进行检查，因为边缘状态的重叠无关紧要，关键在于重要数字与图形之间必须形成一一对应的关系。由于这个图形的长度可以调整，但其中任意一个图形的活动范围都存在限制，而限制条件恰好是其自身长度与区块长度。只有当图形和数字实现一一对应时，这种方法才具备实际意义。基于此，我们也反向推导出了它们必然一一对应的原因，并且可以将这一性质应用到解题过程中。这部分内容同样是为第二章的相关内容所做的铺垫。

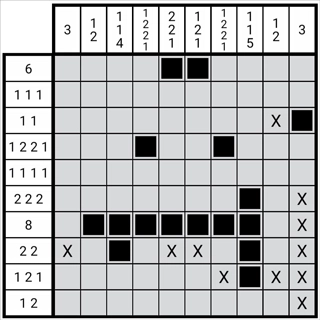
图1-3-4

如图所示，图中第七列第七行的数字2是通过该方法确定的第七列第3个数字，依据位置关系的对应性，第4个数字1的位置必然在第七列第十行。

综上，我们可以归纳出一种快速判定正格的方法：首先从某一排的第一行格起，依次绘制出上述的数字-空格图形；接着从起始方向减去最后剩余的空格数量，若结果为负数则视为零；最终得到的图形必然是正格。此外，这些图形与原图形的位置关系存在对应性，且是运用第一章全部方法所能获取的最多正格，该方法被称作边缘法。

游戏亮点

1、借助像素化逻辑谜题挖掘更多线索，从而揭开其中隐藏的图像

2、纵横数字与文字类游戏简单易上手，都是你熟悉的知识范畴，其玩法极具吸引力，很容易让人沉浸其中。

3、挑选最契合自身的难度，从基础起步逐步提升游戏里的难度等级

小编点评：

趣味填格小游戏，根据两侧的提示来进行填格子。