汉诺塔是一款十分有趣的休闲益智游戏，游戏采用了精致又舒适的卡通画面风格，能让玩家获得更放松的视觉感受。玩家需要按照颜色将杆上的圆柱依次放到正确位置，从而不断闯关，完成游戏任务。玩家还可以借助另外两根杆来辅助移动，并且要遵循规则，按从大到小的顺序叠加圆柱，还能自由切换不同视角，开启精彩的挑战之旅。丰富刺激的挑战，玩家都能持续体验，游戏还有大量关卡等待解锁，后期难度会逐步提升，极大地考验着玩家的脑力极限。精彩有趣的玩法，让整个过程不会枯燥，感兴趣的玩家可别错过，随时都能尽情畅玩。

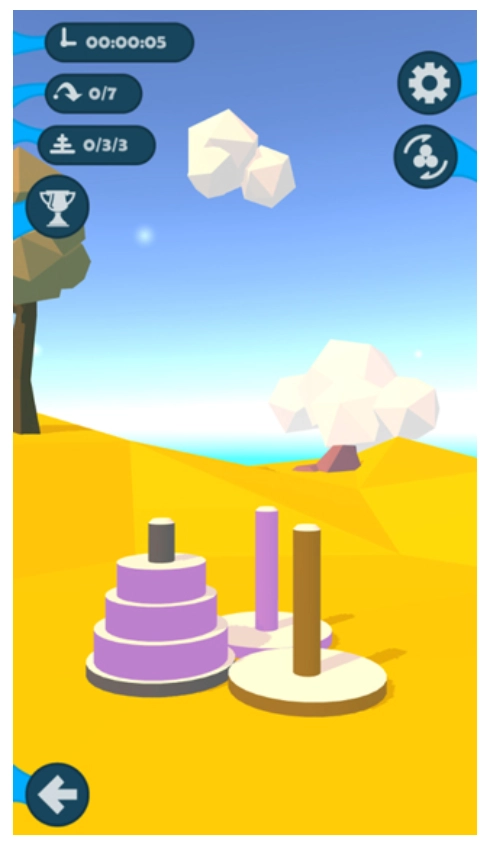
游戏特色

1、放松体验

游戏画面简约清爽，为您带来舒缓的视觉享受，挑战过程轻松无压力，助您顺利完成一个个精彩有趣的任务。

2、惊喜玩法

玩法简单有趣，还融入了不少好玩的模式，更有诸多惊喜玩法等待解锁。

3、挑战关卡

关卡内容十分丰富，玩家将开启一场极限的智力较量，这一过程既考验思维能力，又充满了欢乐氛围。

4、认真思考

在这里只能按顺序依次叠加，过程无法逆转，每一步都需要玩家仔细斟酌。

5、自由比拼

在线的竞技玩法，还能和更多高手玩家一同较量，争夺游戏成就与排名。

6、好玩体验

经典又有趣的休闲游戏，既能锻炼玩家的智力与思维能力，还能解锁各种好玩的内容。

游戏内容

1、玩法就是大家熟悉的汉诺塔游戏，这个游戏源自印度一个古老传说中的益智玩具。游戏里，玩家要在一根柱子上从下到上按大小顺序摞好64片黄金圆盘，看似简单的游戏，玩起来却非常烧脑又刺激。

2、圆盘需从最下方开始，依照大小次序重新放置到另一根柱子上，同时有如下规则：小圆盘上方不能放置大圆盘，三根柱子之间每次仅能移动一个圆盘。这个游戏操作起来不算复杂，但整个过程却十分考验脑力。

3、这款游戏最具趣味性的点在于玩家能够自定义圆块的外形，像五角星、三角形之类的都可以，这大大提升了游戏的可玩性。超多有趣的体验等着您不断解锁，另外还有多种游戏难度可供选择，欢乐无穷。

4、游戏准备了上百个各具特色的关卡等待玩家挑战，每个关卡的难度都有所不同。想要顺利通关，关键在于玩家充分调动自己的脑力，仔细思考并找到高效的解题思路，在完成任务的过程中收获满满的挑战乐趣。

游戏亮点

1、游戏内的所有内容现已全面开放免费体验，你可以毫无限制地畅玩，尽情感受其中的乐趣。

2、玩家以点击的方式进行操作，只要把所有棋子都移到右边的旗杆上就算获胜。

3、玩法和童年玩过的搬砖游戏有点像，玩的时候能让你感受到满满的回忆。

4、海量关卡等待你来挑战，最终能顺利闯过多少关，完全取决于你的操作水平。

游戏玩法

一、汉诺塔玩法如下：

有三根相邻的柱子，它们的颜色依次是墨黑色、棕色和粉紫色。墨黑色柱子上从下往上以金字塔的形状叠放着n个大小各异的粉色圆盘。现在需要把这些圆盘逐个移动到粉紫色柱子上，移动规则是每次只能移动一个圆盘，而且大的圆盘不能放在小的圆盘上面。

二、公式

现在有三根相邻的柱子，分别用墨黑色、棕色、粉紫色标记为A、B、C，A柱子上从下到上呈金字塔状叠放着n个大小各异的圆盘。要求将所有圆盘逐个移动到B柱子上，且每次移动后同一根柱子上都不能出现大盘子压在小盘子上方的情况，那么完成这个任务至少需要多少次移动呢？我们设移动次数为H(n)。

首先我们要做的是把上面n-1个盘子移到柱子C上，接着将最大的那块放在B上，最后再把C上的所有盘子移到B上，通过这样的步骤我们就能得出对应的表达式：

H⑴ = 1

H(n) = 2*H(n-1）+1 (n>1）

那么我们很快就能得到H(n）的一般式：

H(n) = 2^n - 1 (n>0)

而且这种方法确实是移动次数最少的，证明起来十分简单，大家可以试着从2个盘子的移动过程开始验证。