matlab7.0是一款由美国MathWorks公司出品的专业数学软件,作为三大数学软件之一,matlab在数值计算方法的能力首屈一指。用户可以将Matlab7.0破解版用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言,该软件是数学界的计算神器。
1、强大的计算能力
Matlab具有高效的数值计算及符号计算功能,能帮助用户从繁杂的数学运算分析中解脱出来;
2、图形处理功能
Matlab具有完备的图形处理功能,可实现计算结果和编程的可视化,更为直观方便;
3、用户体验
Matlab友好的用户界面及接近数学表达式的自然化语言,创造了极佳的用户体验,使用户更易于学习和掌握;
4、功能齐全
除了基本的计算功能等,Matlab还内置功能丰富的应用工具箱(如信号处理工具箱、通信工具箱等) ,为用户提供了大量方便实用的处理工具。
2、打开下载的虚拟光驱Matlab安装包,并解压,得到一个iso文件。

3、打开“我的电脑”-->找到安装好的虚拟光驱,右击装载。

4、成功载入后,找到软件安装文件“setup.exe”进行安装。
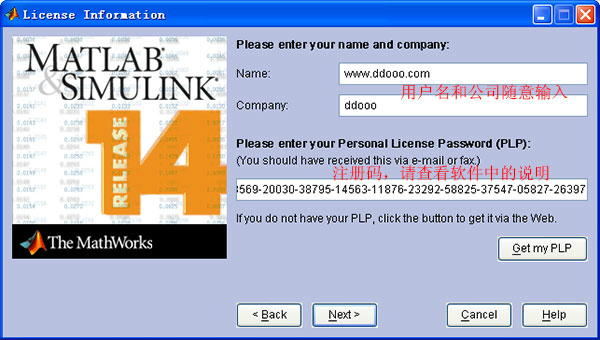
5、选择“install”,再输入用户名,公司名称以及注册码,注册码请在软件官网购买。
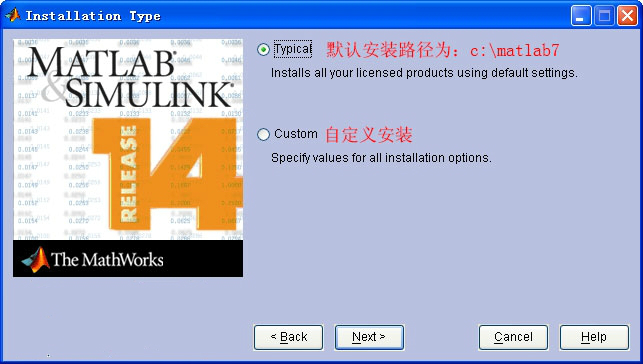
6、再选择“typical”按默认方式安装,也可以选择“custom”自定义安装路径。
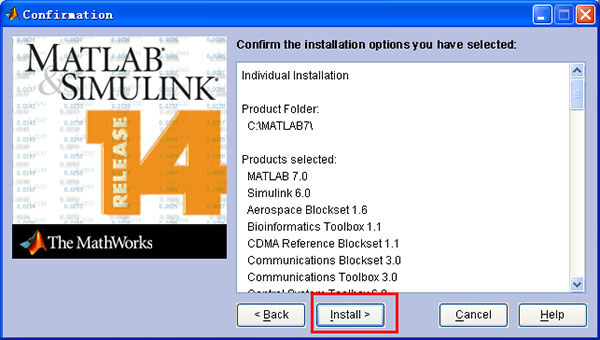
7、点击“install”开始安装。
8、耐心稍等几分钟。
9、完成后,点击“next”按纽。
10、勾选“start matlab”后,点击“finish”即安装完成。
【使用教程】
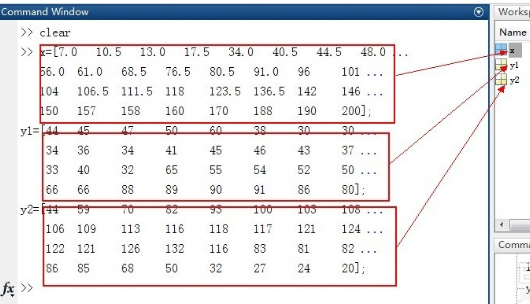
既然要画散点图,自然就需要一些离散的数据了,下面我们就利用matlab生成这些数据,实际应用中我们获得的数据是从其他方式获得的。具体的指令和结果如下图所示:
首先需要先画出点图,即把每一个数据点的位置画出来,所使用的指令为:scatter(x,y1,'k'),该指令主要用于绘制点图,后面''里面的k标示的是每一个点用黑色画出,里面也可以一起添加一些其他的参数:如下图所示:

下面是利用第一步生成的数据和第二步的指令画出的点图,如下图所示,绿色的是y1的数据,红色的是y2的数据。
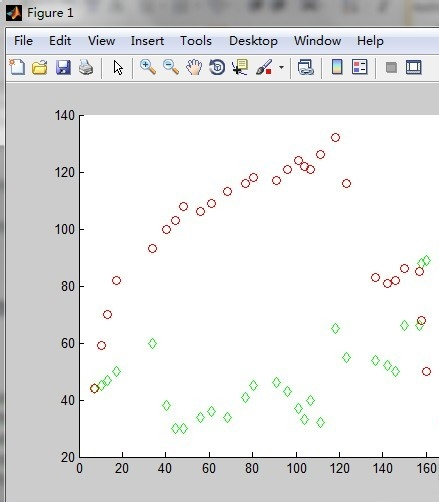
下面就把点串起来,就大功告成了,使用的指令是:plotyy(x,y1,x,y2,'plot');具体的图形如下图所示:

matlab中关于画图函数plot()的简析
plot() 函数是绘制二维图形的最基本函数,它是针对向量或矩阵的列来绘制曲线的。使用plot 函数之前,必须首先定义好曲线上每一点的x 及y 坐标.下面简单介绍!
plot(x) 当x 为一向量时,以x 元素的值为纵坐标,x 的序号为横坐标值绘制曲线。当x 为一实矩阵时,则以其序号为横坐标,按列绘制每列元素值相对于其序号的曲线
例如:此处用
x=0:pi/20:2*pi;
y1=sin(x);
plot(x,y1);
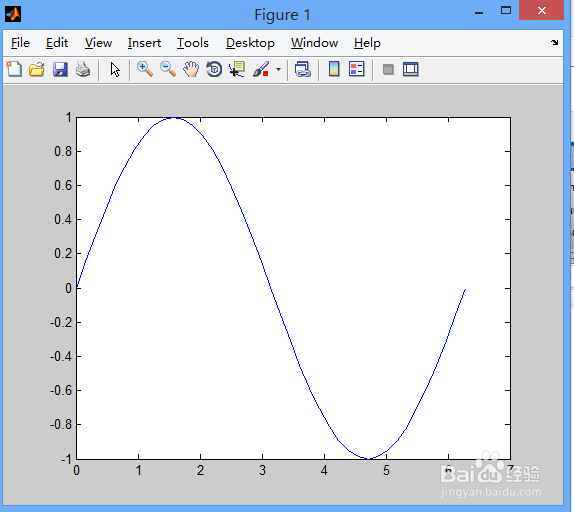
1, plot(x,y) 以x 元素为横坐标值,y 元素为纵坐标值绘制曲线。
2, plot(x,y1,x,y2,…) 以公共的x 元素为横坐标值,以y1,y2,… 元素为纵坐标值绘制多条曲线。
x=0:pi/20:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,x,y2);
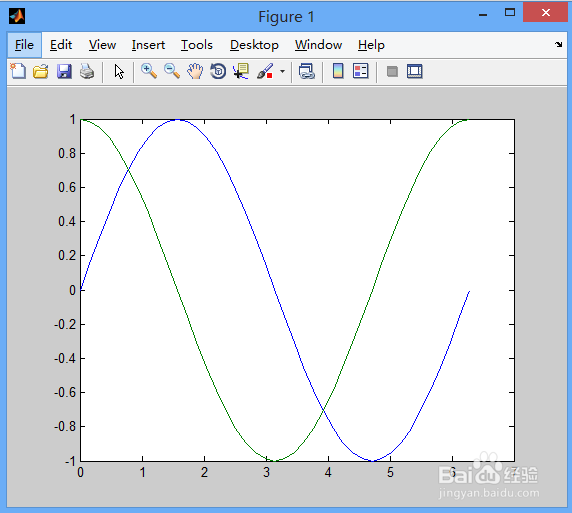
可以在画的图像中添加栅格,用命令grid on,这样可以方便你对齐某条线或是对比比较方便,看下图可以上图对比,看下有什么不同,测试代码如下:
x=0:pi/20:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,x,y2);
grid on
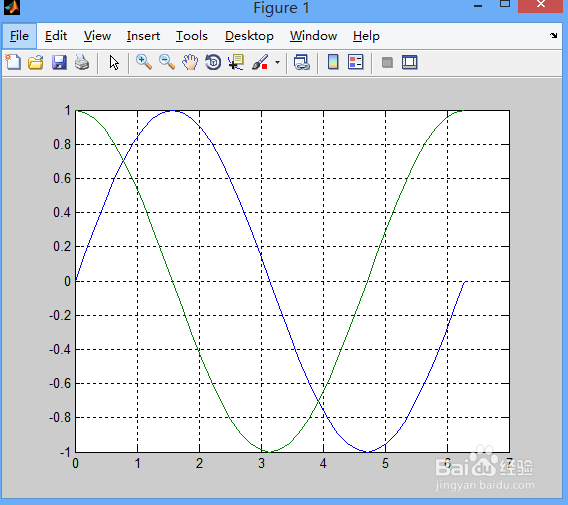
添加坐标轴信息,这样做可以很快的让人明白你在做什么,测试代码如下
x=0:pi/20:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,x,y2);
grid on
xlabel('变量 X')
ylabel('变量 Y1 & Y2')
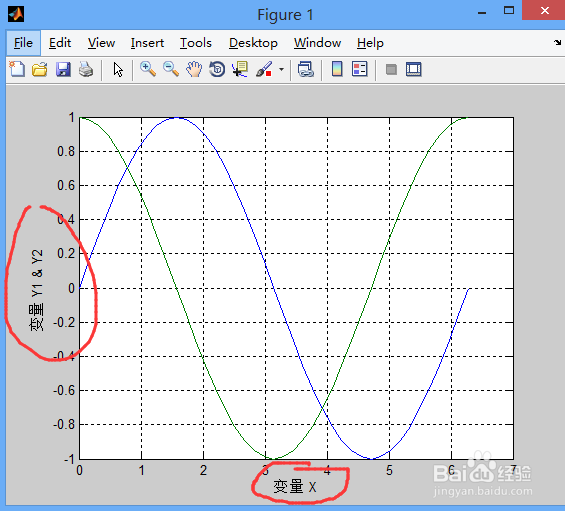
除了坐标轴信息外还可以添加其它的信息,如所画曲线的信息等:测试代码如下
x=0:pi/20:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,x,y2);
grid on
xlabel('变量 X')
ylabel('变量 Y1 & Y2')
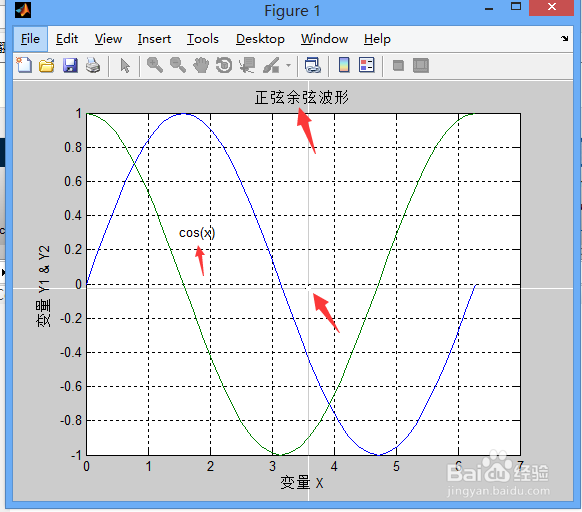
title('正弦余弦波形') %添加图像标题
text(1.5,0.3,'cos(x)') %将cosx这个注解加到坐标中的某个位置
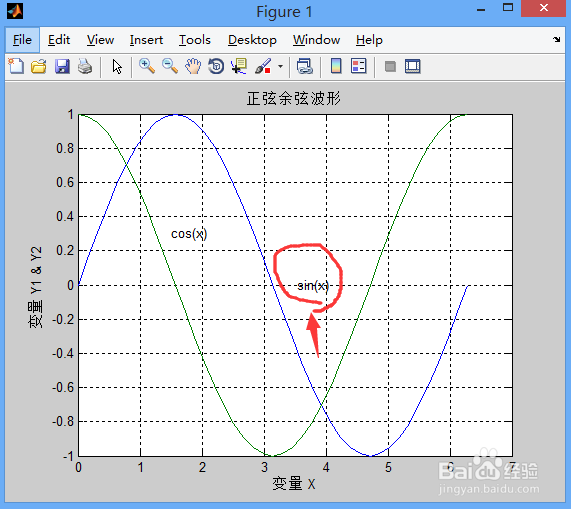
gtext('sin(x)') % 用鼠标的光标定位,将sinx这个注解放在你鼠标点击的地方
通过各图的对比,你就会发现这些命令的用法
b blue 蓝 . point - solid
g green 绿 o circle : dotted
r red 红 x x-mark -. dashdot
c cyan 青 + plus -- dashed
m magenta 品红 * star (none) no line
y yellow 黄 s square
k black 黑 d diamond
w white 白 v triangle (down)
^ triangle (up)
< triangle (left)
> triangle (right)
p pentagram 五角星
h hexagram 六角星
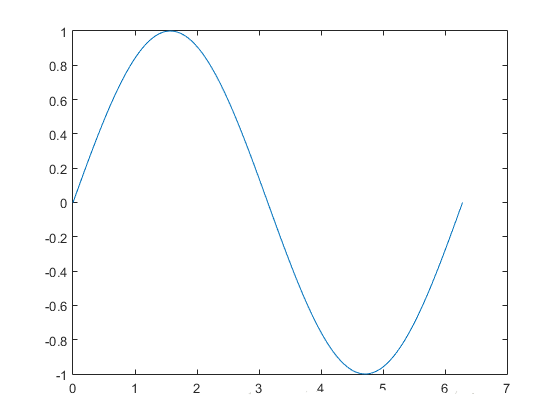
2,plot(x,y):创建2维直线图。例如(以下代码都是在command窗口敲的):
>> x = 0:pi/100:2*pi;
>> y = sin(x);
>> plot(x,y)
图示:
3,plot(X1,Y1,...,Xn,Yn):画n条线。例如:
>> x = linspace(-2*pi,2*pi);
>> y1 = sin(x);
>> y2 = cos(x);
>> plot(x,y1,x,y2)
图示:
4,plot(Y):Y是矩阵,这表示矩阵的每一行都画一条线。例如:
>> Y = magic(4); % 这是一个4*4的矩阵,详情请在command窗口输入help magic查看
>> plot(Y)
图示:
5,plot(x,y1, x,y2,'--', x,y3,':'):画三条不同风格的线,‘’中的内容可以改为第1小节的其他线条。例子如下:
>> x = 0:pi/100:2*pi;
>> y1 = sin(x);
>> y2 = sin(x-0.25);
>> y3 = sin(x-0.5);
>> plot(x,y1,x,y2,'--',x,y3,':')
图示:
6,plot(x,y1,'g',x,y2,'b--o',x,y3,'c*'):特殊的线条和颜色组合,引号内的就是颜色和线条,可以由第1小节的颜色和线条自由组合。例如:
>> x = 0:pi/10:2*pi;
>> y1 = sin(x);
>> y2 = sin(x-0.25);
>> y3 = sin(x-0.5);
>> plot(x,y1,'g',x,y2,'b--o',x,y3,'c*')
图示:
7,线宽调整
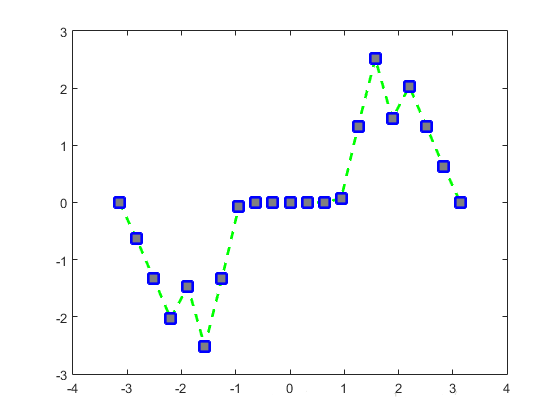
plot(x,y,'--gs','LineWidth',2,'MarkerSize',10,'MarkerEdgeColor','b','MarkerFaceColor',[0.5,0.5,0.5])
这里'--gs'表示用方框画点,然后用绿色虚线连结;'LineWidth',2表示绿色虚线宽度为2;'MarkerSize',10表示方框大小为10;'MarkerEdgeColor','b'表示方框边缘颜色为蓝色;'MarkerFaceColor',[0.5,0.5,0.5]表示方框填充色为[0.5,0.5,0.5](这是RGB颜色值)。例如:
>> x = -pi:pi/10:pi;
>> y = tan(sin(x)) - sin(tan(x));
>> plot(x,y,'--gs','LineWidth',2,'MarkerSize',10,'MarkerEdgeColor','b','MarkerFaceColor',[0.5,0.5,0.5])
图示:
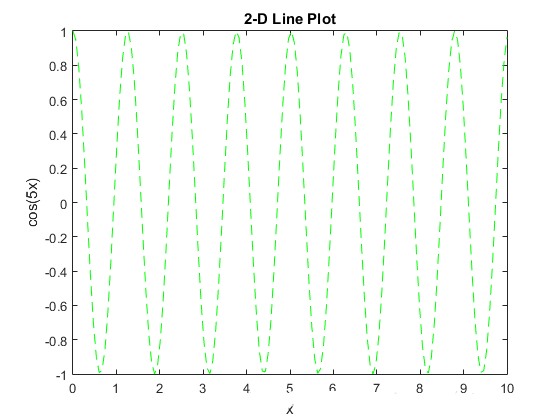
8,标题和坐标轴标签,例如:
>> x = linspace(0,10,150);
>> y = cos(5*x);
>> plot(x,y,'--g')
>> title('2-D Line Plot')
>> xlabel('x')
>> ylabel('cos(5x)')
图示:
9,绘制子图,点这里有详细的讲解。这里还是举个例子:
>> ax1 = subplot(2,1,1); % top subplot
>> ax2 = subplot(2,1,2); % bottom subplo
图示:
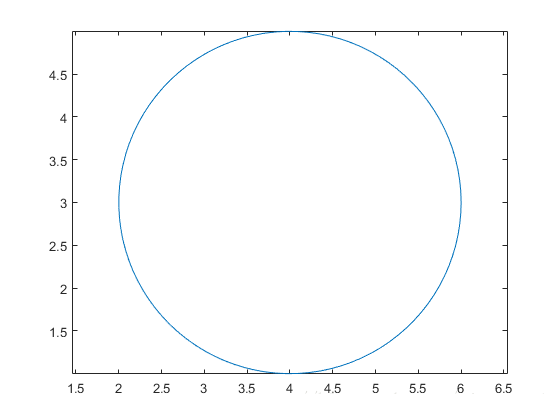
10,画圆。例子:
r = 2; % 半径
xc = 4; % (xc,yc)是圆心坐标
yc = 3;
theta = linspace(0,2*pi);
x = r*cos(theta) + xc;
y = r*sin(theta) + yc;
plot(x,y)
axis equal % 把x,y轴设为等距,以便于更好地显示圆。
图示:
1.前言
求解方程是工科学习和工程计算中最基础、最常见的问题。掌握利用现代化工具求解方程的方法对于提升我们的工科素养至关重要。为此,本篇将对matlab中求解方程的方法进行介绍。
2.用法

2.1 指明变量
告诉电脑方程中所含有的变量,包括参数和未知变量。比如:所求解的方程为:,很显然该方程中有a,b,c,x符号变量,因此该步骤的写法为:
syms a b c x
2.2 指明方程,未知数和限制条件(非必需)
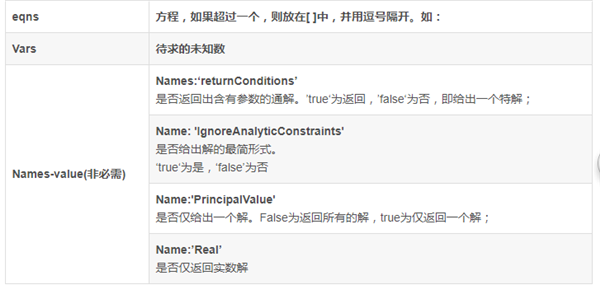
2.3 获得所求方程的解
如果为多个函数,该解存储形式为结构体。
3.具体实例
3.1求解sin(x)=1的通解
具体代码:
syms x
[x,params,conds]=solve(sin(x)==1,'ReturnConditions', true)
结果
solx =pi/2+2*pi*k
params =k
conds =in(k,'integer')
可以看出,该方程的通解为:

3.2求解以下方程:
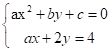
代码:
syms a b c y x
[x,y]=solve([a*x^2+b*y+c==0,a*x+2*y==4],[x,y])
结果:
x =
((a*b)/4-(-(a*(- a*b^2+32*b +16*c))/16)^(1/2))/a
((a*b)/4+(-(a*(- a*b^2+32*b +16*c))/16)^(1/2))/a
y =
(-(a*(- a*b^2+32*b +16*c))/16)^(1/2)/2-(a*b)/8+2
2-(-(a*(- a*b^2+32*b +16*c))/16)^(1/2)/2-(a*b)/8
即:
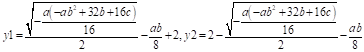
1.解方程、方程组
x^2-4=12,求x:
syms x;
f=x^2-4-12;
solve(f)
最近有多人问如何用matlab解方程组的问题,其实在matlab中解方程组还是很方便的,例如,对于代数方程组Ax=b(A为系数矩阵,非奇异)的求解,MATLAB中有两种方法:
(1)x=inv(A)*b — 采用求逆运算解方程组;
(2)x=A\B — 采用左除运算解方程组
PS:使用左除的运算效率要比求逆矩阵的效率高很多~
例:
x1+2x2=8
2x1+3x2=13
>>A=[1,2;2,3];b=[8;13];
>>x=inv(A)*b
x =
2.00
3.00
>>x=A\B
x =
2.00
3.00;
即二元一次方程组的解x1和x2分别是2和3。
对于同学问到的用matlab解多次的方程组,有符号解法,方法是:先解出符号解,然后用vpa(F,n)求出n位有效数字的数值解.具体步骤如下:
第一步:定义变量syms x y z ...;
第二步:求解[x,y,z,...]=solve('eqn1','eqn2',...,'eqnN','var1','var2',...'varN');
第三步:求出n位有效数字的数值解x=vpa(x,n);y=vpa(y,n);z=vpa(z,n);...。
如:解二(多)元二(高)次方程组:
x^2+3*y+1=0
y^2+4*x+1=0
解法如下:
>>syms x y;
>>[x,y]=solve('x^2+3*y+1=0','y^2+4*x+1=0');
>>x=vpa(x,4);
>>y=vpa(y,4);
结果是:
x =
1.635+3.029*i
1.635-3.029*i
-.283
-2.987
y =
1.834-3.301*i
1.834+3.301*i
-.3600
-3.307。
二元二次方程组,共4个实数根;
还有的同学问,如何用matlab解高次方程组(非符号方程组)?举个例子好吗?
解答如下:
基本方法是:solve(s1,s2,…,sn,v1,v2,…,vn),即求表达式s1,s2,…,sn组成的方程组,求解变量分别v1,v2,…,vn。
具体例子如下:
x^2 + x*y + y = 3
x^2 - 4*x + 3 = 0
解法:
>> [x,y] = solve('x^2 + x*y + y =3','x^2 - 4*x + 3 = 0')
运行结果为
x =
1 3
y =
1 -3/2
即x等于1和3;y等于1和-1.5
或
>>[x,y] = solve('x^2 + x*y + y =3','x^2 - 4*x + 3= 0','x','y')
x =
1 3
y =
1 -3/2
结果一样,二元二方程都是4个实根。
通过这三个例子可以看出,用matlab解各类方程组都是可以的,方法也有多种,只是用到解方程组的函数,注意正确书写参数就可以了,非常方便。
2、变参数非线性方程组的求解
对于求解非线性方程组一般用fsolve命令就可以了,但是对于方程组中某一系数是变化的,该怎么求呢?
%定义方程组如下,其中k为变量
function F = myfun(x,k)
H=0.32;
Pc0=0.23;W=0.18;
F=[Pc0+H*(1+1.5*(x(1)/W-1)-0.5*(x(1)/W-1)^3)-x(2);
x(1)-k*sqrt(x(2))];
%求解过程
H=0.32;
Pc0=0.23;W=0.18;
x0 = [2*W; Pc0+2*H]; % 取初值
options = optimset('Display','off');
k=0:0.01:1; % 变量取值范围[0 1]
for i=1:1:length(k)
kk=k(i);
x = fsolve(@(x) myfun(x,kk), x0, options);%求解非线性方程组
x1(i)=x(1);
x2(i)=x(2);
end
plot(k,x1,'-b',k,x2,'-r');
xlabel('k')
legend('x1','x2')
3、非线性方程数值求解
matlab里solve如何使用,是否有别的函数可以代替它.
matlab里我解y=9/17*exp(-1/2*t)*17^(1/2)*sin(1/2*17^(1/2)*t)=0这样的方程为什么只得到0这一个解,如何可以的到1/2*17^(1/2)*t=n*(pi)这样一族解??
在matlab里面solve命令主要是用来求解代数方程(即多项式)的解,但是也不是说其它方程一个也不能解,不过求解非代数方程的能力相当有限,通常只能给出很特殊的实数解。(该问题给出的方程就是典型的超越方程,非代数方程)
从计算机的编程实现角度讲,如今的任何算法都无法准确的给出任意非代数方程的所有解,但是我们有很多成熟的算法来实现求解在某点附近的解。matlab也不例外,它也只能给出任意非代数方程在某点附近的解,函数有两个:fzero和fsolve,具体用法请用help或doc命令查询吧。如果还是不行,你还可以将问题转化为非线性最优化问题,求解非线性最优化问题的最优解,可以用的命令有:fminbnd,fminsearch, fmincon等等。
*非线性方程数值求解
*单变量非线性方程求解
在MATLAB中提供了一个fzero函数,可以用来求单变量非线性方程的根。该函数的调用格式为:
z=fzero('fname',x0,tol,trace)
其中fname是待求根的函数文件名,x0为搜索的起点。一个函数可能有多个根,但fzero函数只给出离x0最近的那个根。tol控制结果的相对精度,缺省时取tol=eps,trace?指定迭代信息是否在运算中显示,为1时显示,为0时不显示,缺省时取trace=0。
例 求f(x)=x-10x+2=0在x0=0.5附近的根。
步骤如下:
(1) 建立函数文件funx.m。
function fx=funx(x)
fx=x-10.^x+2;
(2) 调用fzero函数求根。
z=fzero('funx',0.5)
z =
0.3758
**非线性方程组的求解
对于非线性方程组F(X)=0,用fsolve函数求其数值解。fsolve函数的调用格式为:
X=fsolve('fun',X0,option)
其中X为返回的解,fun是用于定义需求解的非线性方程组的函数文件名,X0是求根过程的初值,option为最优化工具箱的选项设定。最优化工具箱提供了20多个选项,用户可以使用optimset命令将它们显示出来。如果想改变其中某个选项,则可以调用optimset()函数来完成。例如,Display选项决定函数调用时中间结果的显示方式,其中‘off’为不显示,‘iter’表示每步都显示,‘final’只显示最终结果。optimset(‘Display’,‘off’)将设定Display选项为‘off’。
例 求下列非线性方程组在(0.5,0.5) 附近的数值解。
(1) 建立函数文件myfun.m。
function q=myfun(p)
x=p(1);
y=p(2);
q(1)=x-0.6*sin(x)-0.3*cos(y);
q(2)=y-0.6*cos(x)+0.3*sin(y);
(2) 在给定的初值x0=0.5,y0=0.5下,调用fsolve函数求方程的根。
x=fsolve('myfun',[0.5,0.5]',optimset('Display','off'))
x =
0.6354
0.3734
将求得的解代回原方程,可以检验结果是否正确,命令如下:
q=myfun(x)
q =
1.0e-009 *
0.2375 0.2957
可见得到了较高精度的结果。
4、fsolve函数解方程
[X,FVAL,EXITFLAG,OUTPUT,JACOB]=FSOLVE(FUN,X0,...) returns the
Jacobian of FUN at X.
Examples
FUN can be specified using @:
x = fsolve(@myfun,[2 3 4],optimset('Display','iter'))
where myfun is a MATLAB function such as:
function F = myfun(x)
F = sin(x);
FUN can also be an anonymous function:
x = fsolve(@(x) sin(3*x),[1 4],optimset('Display','off'))
If FUN is parameterized, you can use anonymous functions to capturethe
problem-dependent parameters. Suppose you want to solve the systemof
nonlinear equations given in the function myfun, which isparameterized
by its second argument c. Here myfun is an M-file function suchas
function F = myfun(x,c)
F = [ 2*x(1) - x(2) - exp(c*x(1))
-x(1) + 2*x(2) - exp(c*x(2))];
To solve the system of equations for a specific value of c, firstassign the
value to c. Then create a one-argument anonymous function thatcaptures
that value of c and calls myfun with two arguments. Finally, passthis anonymous
function to FSOLVE:
c = -1; % define parameter first
x = fsolve(@(x) myfun(x,c),[-5;-5])
【举例解一元方程】
先举一例,解方程“x^2+100*x+99=0”。
在Matlab ”Command Window“中输入如下命令:x=solve(‘x^2+100*x+99=0’,‘x’),见下图。
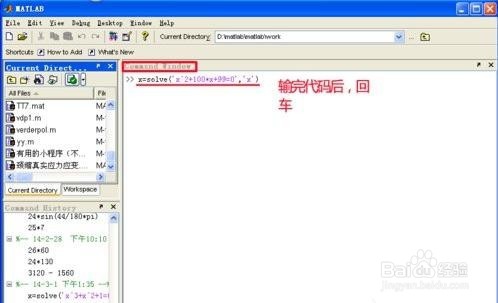
2、回车后,Matlab就求出了这个一元二次方程的解,见下图。
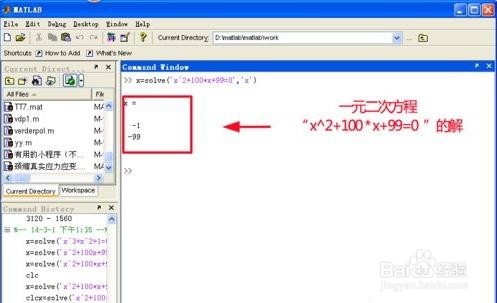
再举一例,解一元三次方程“x^3+1=0”。
在Matlab ”Command Window”中输入如下命令:x=solve(‘x^3+1=0’,‘x’),见下图。
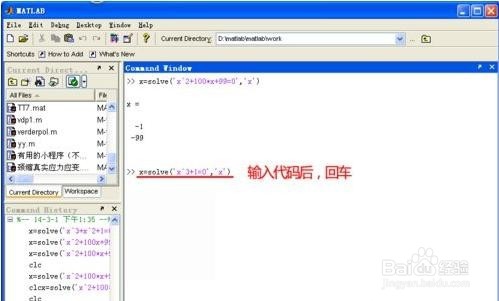
回车后,Matlab就求出了这个一元三次方程“x^3+1=0”的解,见下图。
Matlab解出来的解有三个,其中有一个实数解,两个虚数解。
我们都知道一元三次方程在复数范围内的解有3个,Matlab的解是对的。
如果我们只要“x^3+1=0”的实数解,我们只要取下面图中的第一个解“-1”。
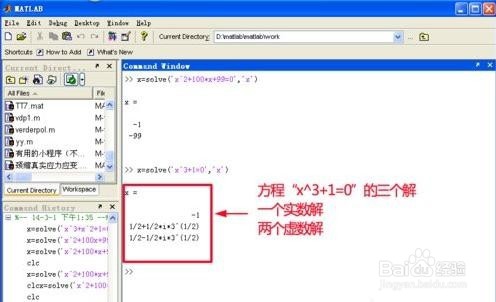
【举例解二元一次方程】
首先来求一个二元一次方程组。
9x+8y=10 式1
13x+14y=12 式2
我们一般的解法是代入法,或者加减消去法。比较繁琐。
这里我们只需输入如下命令即可求出解:[x,y]=solve(‘9*x+8*y=10’,‘13*x+14*y=12’,‘x’,‘y’)。
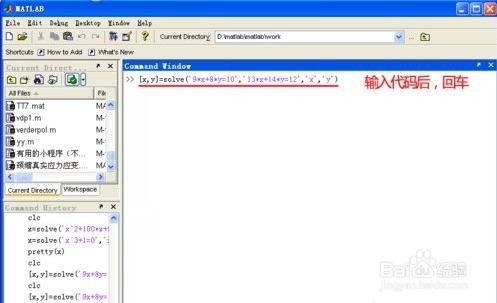
回车后,Matlab就求出了这个二元一次方程组的解,见下图。
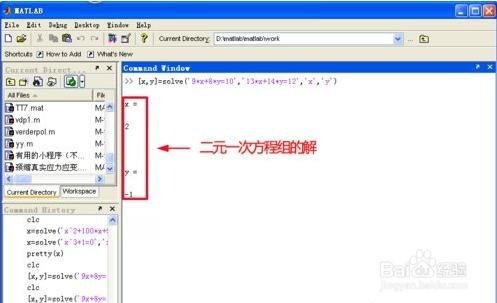
再来求一个二元非线性方程组
x^2+y^2=10 式1
2x+3y=0 式2
这里我们只需输入如下命令即可求出解:[x,y]=solve(‘x^2+y^2=10’,‘2*x+3*y=0’,‘x’,‘y’)。
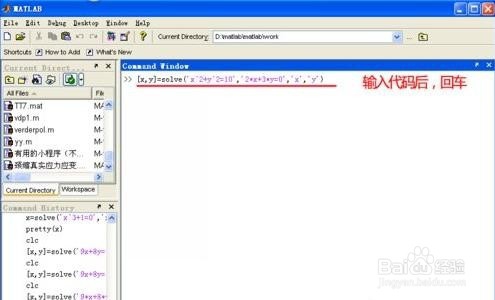
x^2+y^2=10 式1
2x+3y=0 式2
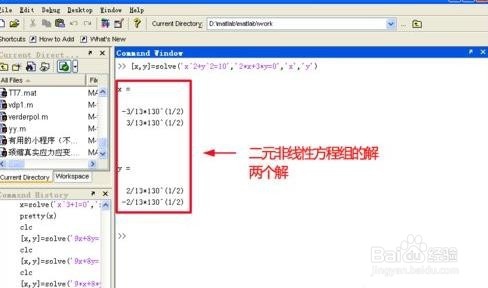
其实不少人能看出来,上面的二元非线性方程组的解是一个圆与一条直线的交点坐标,我们的一般解法是先消去y,整理成关于x的一元二次方程,然后求出x值,再求出对应y值。
但这里,我们只用到了上面图片里的的一句命令,就求了这两个交点坐标,见下图。
例1:求y=3*sin(x)+4*x^2的导数
syms x;
diff(3*sin(x)+4*x^2)
例2:求y=ln(x+cos(x))
syms x;
diff(log(x+cos(x)))
求一组一元函数的导数:
例3:求f(x)={sin(x)+1;
cos(x)+x;
4*x^4}的导数
syms x;
diff([sin(x)+1,cos(x)+x,4*x^4])
求一元函数的高阶导数:
例4:求y=3*sin(x)+4*x^8的7阶导数
syms x;
diff(3*sin(x)+4*x^8,7)
参数方程形式的函数求导:
例5:已知{x=t^2-ln(2+sint)
{y=t^3-3*sin(ln(t)),求dy/dx。
syms t;
dx_dt=diff(t^2+log(2+sin(t)));
dy_dt=diff(t^3+3*sin(log(t)));
dy_dx=dy_dt/dx_dt
求函数的极值和最值:
例6:计算f(x)在区间[a,b]内的最小值点x和最小值f。
[x,f]=fminbnd('x^2-3*x+1',-10,10)
例7:求函数在某一点附近的局部最小值和最小值点。
[x,f]=fminsearch('sin(2*x)+1',5)
经常出现类似这样的问题,一般是路径设置不对,如何设置默认的路径,可以用file-save path
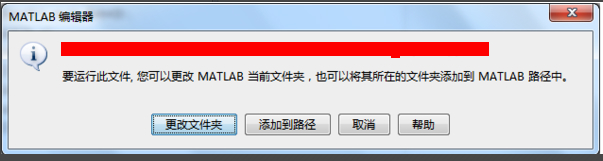
设置路径前,你要先看你现在的文件是哪个路径下,怎么看呢,如下图所示,一个是命令窗口下的文件路径,一个是M文件,也就是函数文件所在目录,如果这个M文件的函数是你自己写的一样要和工程路径放在一起,不然,在调用时就会出错!
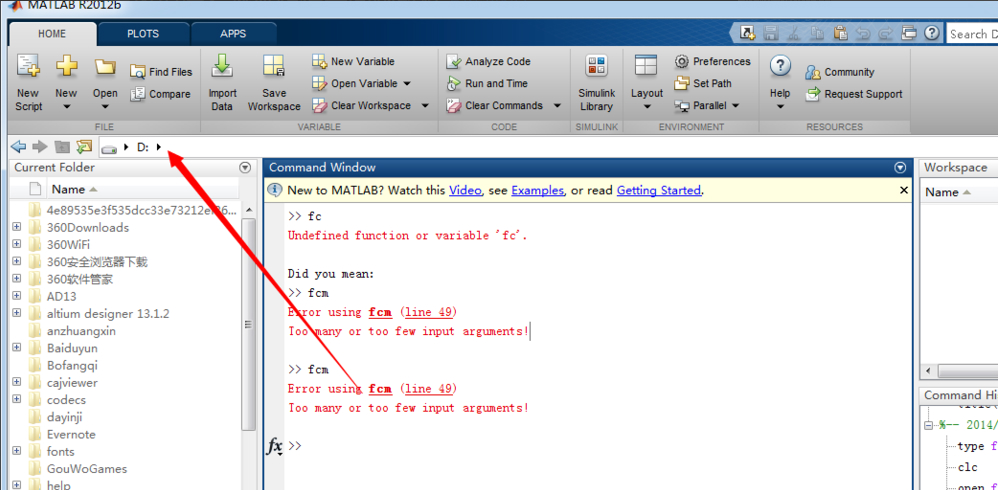

出现Undefined function or variable怎么解决?
出现这种问题的原因,一是你的函数调用时写错了,二是你确实使用了未定义或是不存在的函数,三就是上面所的问题,即路径设置不对
还有一个原因,就是函数在保存的时候设置不对,例如下面所示几种函数名都是不对,函数名的保存必须要与你定义的函数名字保持一样或是定义的主函数名一样,函数名不能有“.” 、“-”、或是数字开头,这些字符在函数名中都能导致这种错误

怎么解决fcm错误?
有时直接运行自带函数会出现下面的错误是正常,因为你未正常的调用函数,未赋值给函数所以会出现这样的错误,一旦你正常的调用后,这种错误就会消失


【软件特色】
软件特色:1、强大的计算能力
Matlab具有高效的数值计算及符号计算功能,能帮助用户从繁杂的数学运算分析中解脱出来;
2、图形处理功能
Matlab具有完备的图形处理功能,可实现计算结果和编程的可视化,更为直观方便;
3、用户体验
Matlab友好的用户界面及接近数学表达式的自然化语言,创造了极佳的用户体验,使用户更易于学习和掌握;
4、功能齐全
除了基本的计算功能等,Matlab还内置功能丰富的应用工具箱(如信号处理工具箱、通信工具箱等) ,为用户提供了大量方便实用的处理工具。

【安装教程】
1、首先下载安装DVDFab Virtual Drive虚拟光驱,并双击exe文件安装好。
2、打开下载的虚拟光驱Matlab安装包,并解压,得到一个iso文件。

3、打开“我的电脑”-->找到安装好的虚拟光驱,右击装载。

4、成功载入后,找到软件安装文件“setup.exe”进行安装。

5、选择“install”,再输入用户名,公司名称以及注册码,注册码请在软件官网购买。

6、再选择“typical”按默认方式安装,也可以选择“custom”自定义安装路径。

7、点击“install”开始安装。

8、耐心稍等几分钟。

9、完成后,点击“next”按纽。

10、勾选“start matlab”后,点击“finish”即安装完成。


【使用教程】
Matlab教程:
matlab画图基本教程
1.在命令窗口输入命令时,可以不必每输入一条命令就按enter键执行,可以在输入几行后一同运行。方法是:换行时,只要在按住键的同时按键即可,否则matlab就会执行上面输入的所有语句。
2.如何将数据文件导入matlab中并画图:点击file中import data,然后就可以导入文件,然后再workspace里面,点击该数据文件,就可以出现以下图形:
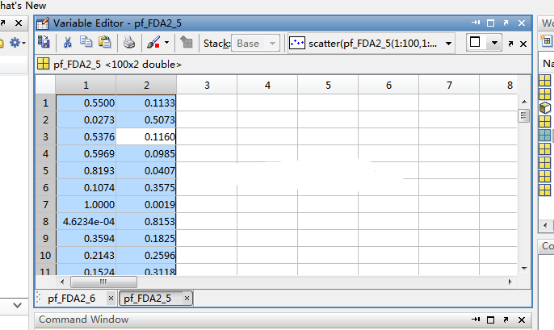
选择该两列,就可以看到在上面有一个scatter然后点击,就可以出现以下图形:
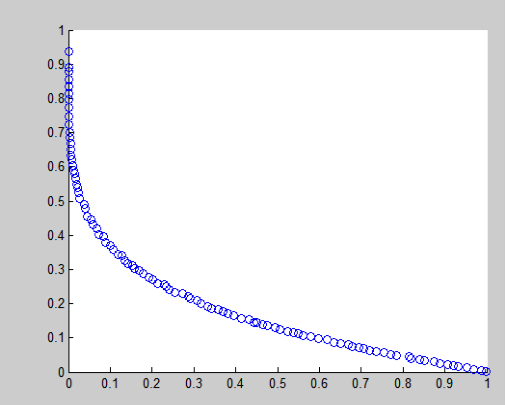
3.分号“;”的作用:用做矩阵(数组)的行间分隔符,用做不显示计算结果的命令。
4.稀疏矩阵
定义:矩阵大部分元素是0,少部分元素是非零元素,这种矩阵是稀疏矩阵。
S=sparse(A);
full(S);
nnz(S);
spy(S);
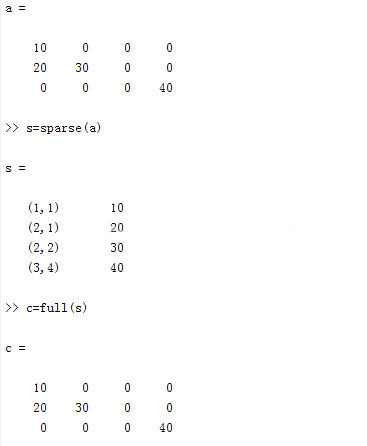
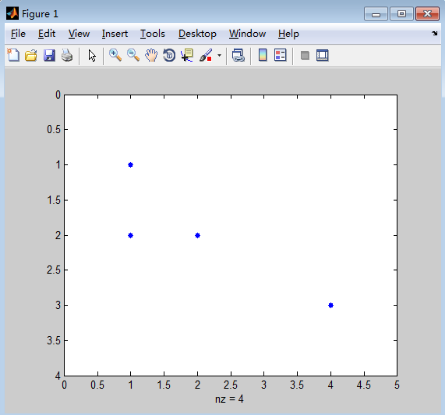
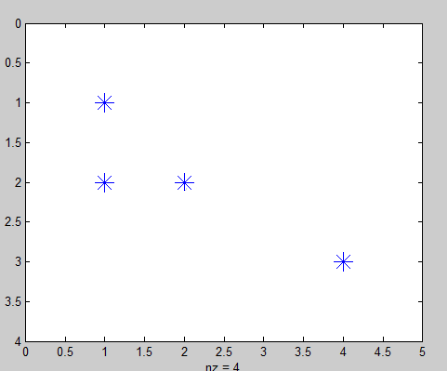
spy(s,,‘*’,16) 表示用’*’号显示,大小为16。如图:
5.注意矩阵的乘法A*B和A.*B的区别:A*B就是A与B的直接相乘,如果是A.*B就是A与B中的对应项相乘。 “./”也是一样的,就是对应项相除。
6.奇异矩阵就是方阵并且行列式为0的矩阵。
7.二维图像绘制
(1)基本函数绘制 ?plot 既可以绘制实线,也可以绘制点线。
<1> plot(X,Y) ?%X,Y为同维向量时,绘制以X、Y元素为横,纵坐标的一条线;X为列向量,Y为矩阵时,按Y列绘制多条不同颜色的曲线,X为这些曲线共同的横坐标。
<2> plot(X,Y,LineSpec) %参数LineSpec用于指出线条的类型,标记符号和颜色。
<3> plot(X1,Y1,LineSpec1,X2,Y2,LineSpec2...) %当Xi和Yi成对出现时,将分别按顺序取两数据Xi和Yi进行画图。
<4> plot(..., ‘PropertyName’,PropertyValue,...)%对图形对象中指定的属性进行设置。
For example:
??x=0:0.1:2;
??y=1+exp(x);
??Plot(x,y, ‘-+b’)
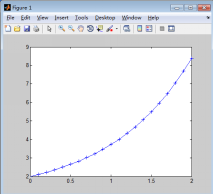
其中,‘-’表示实线,‘+’表示点类型,b表示蓝色。
t=[-pi:pi/100:2*pi]’;k=1:6; y=sin(t)*k;
Plot(t,y) ??%y是矩阵形式
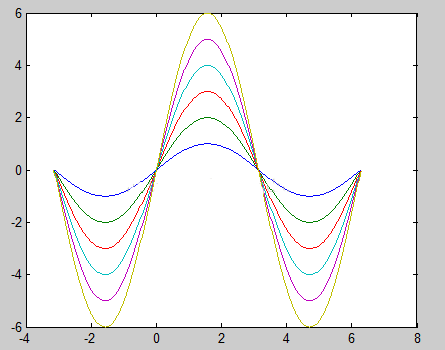
(2)图形标注
<1> 坐标轴名
格式:xlabel(‘string’)
Ylabel(‘string’)
分别给x轴和y轴添加标签
<2> 图名
格式:title(‘string’) 在当前坐标轴上方正中央放置字符串string做为标题。
<3> 图例
格式:legend(‘string1’,’string2’,...)
用指定文字给当前坐标轴添加图例。
For example:
t=0:pi/100:pi;
y1=sin(t);y2=sin(-t);
y3=sin(t).*sin(5*t);
plot(t,y1, ‘-.r’,t,y2, ‘-.k’,t,y3, ‘-bo’)
xlabel(‘时间’);ylabel(‘幅度’);
Title(‘波形及包络线’);
Legend(‘y=sint’, ‘y=-sint’, ‘y=sinsin5t’)
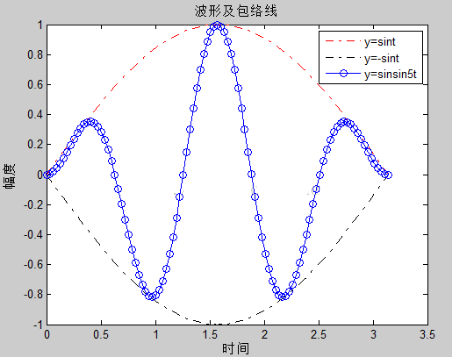
上面的图形标注都是使用标注函数直接写在程序中的,当执行程序后,图形中会自动添加图形标注。但是我们也可以根据图形菜单进行标注,打开图形窗口(Figure)菜单栏中的insert菜单,这时候就可以在图像上添加标注。
(3)图像控制命令
<1>clf %清除所有当前图像窗口
(4)迭加绘图
<1>hold on%保留当前图像与当前坐标轴的属性值,使用后面的图形命令只能在当前存在的坐标轴中增加图形。
<2>hold off %在绘制新图形之前,重新设置坐标轴的属性为默认值,关闭hold on功能。
<3>hold%在on和off之间切换,即在增加图形和覆盖图形之间切换。
<4>hold all %保留当前颜色和线型,在绘制随后的图形时使用当前颜色和线型。
For example:
x=linspace(0,2*pi,60);y=sin(x);
plot(x,y,’b’);
xlabel(‘自变量’),ylabel(‘因变量’);
Hold on;
z=0.5*sin(x);
plot(x,z,’k:’);
legend(‘y=sin(x)’,’z=0.5*sin(x)’);
hold off
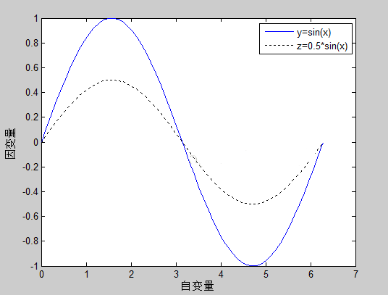
(5)多子图
在同一图形框内布置几幅独立的子图。
格式:subplot(m,n,k) %将一个图形窗口分成m*n个小窗口(子图),k是子图的编号。序号原则是:左上方的为第一幅,然后向右、向下依次排好。
subplot(‘Position’,[left bottom width height]) %在由4个元素指定的位置上创建坐标轴。
x=-4:0.1:4;
subplot(2,2,1);
y1=1/sqrt(2*pi)*exp(-1/2*x.^2),plot(x,y1);
xlabel('变量x'),ylabel('变量密度y'),title('正太分布N(0,1)');
subplot(2,2,2);
y2=1/sqrt(2*pi)/2*exp(-1/2/4*x.^2),plot(x,y2);
xlabel('变量x'),ylabel('概率密度y')
title('正太分布N(0,4)');
subplot(2,2,3);
y3=1/sqrt(2*pi)/0.5*exp(-1/2/(0.5^2)*(x-1).^2),plot(x,y3);
xlabel('变量x'),ylabel('概率密度y'),title('正太分布N(1,1/4)');
subplot(2,2,4);
y4=1/sqrt(2*pi)/0.5*exp(-1/2/(0.5^2)*(x+1).^2),plot(x,y4)
xlabel('变量x'),ylabel('概率密度y'),title('正太分布N(-1,1/4)')
(6)多个图形窗口
格式: Figure(n) %创建新的图形窗口或显示当前图形窗口。n是这个窗口的编号,figure(1)是默认值,不需要声明。
>> t=-4:0.1:4;x=sin(t);plot(t,x,'b^')
>> t=-4:0.1:4;x=sin(t);plot(t,x,'b^')
>> xlabel('t');ylabel('x');title('函数x=sint的图形');
>> figure(2)
>> y=cos(t);plot(t,y,'kp');
>> xlabel('t');ylabel('y');title('函数y=cost的图形');
>> figure(3)
>> z=sin(t).*cos(t);plot(t,z,'kh')
>> xlabel('t');ylabel('z');title('函数z=sincost的图形')
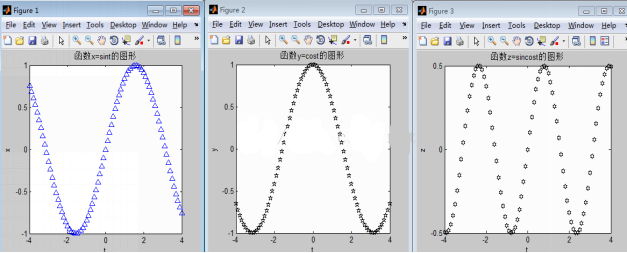
(7)对数比例坐标轴
loglog(x,y) %双对数坐标,在x轴,y轴按对数比例绘制二维图形。
Semilogx %半对数坐标,在x轴按对数比例,y轴按线型比例绘制二维图形。
Semilogy %半对数坐标,在y轴按对数比例,x轴按线型比例绘制二维图形。
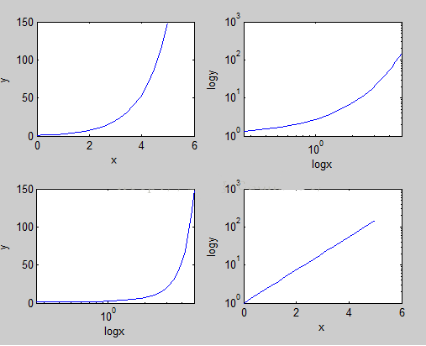
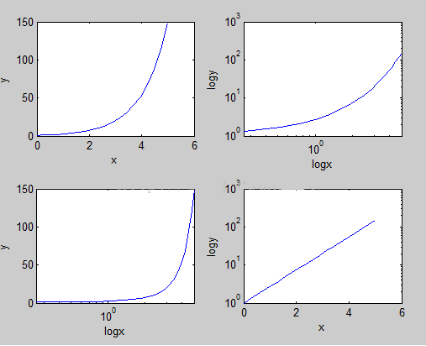
x=linspace(0,5,20);y=exp(x);
>> subplot(2,2,1),plot(x,y),xlabel('x'),ylabel('y');
>> subplot(2,2,2),loglog(x,y),xlabel('logx'),ylabel('logy');
>> subplot(2,2,3),semilogx(x,y),xlabel('logx'),ylabel('y');
>> subplot(2,2,4),semilogy(x,y),xlabel('x'),ylabel('logy');
>>
(8)双纵坐标图
格式:plotyy(x1,y1,x2,y2) %绘制双纵坐标二维图形,x1和y1所对应的图形的纵坐标标注在图形的左边,x2和y2所对应图形的纵坐标标注在图形的右边。
>> x=0:0.1:4;y=x.*sin(x);s=sin(x)-x.*cos(x);
>> plotyy(x,y,x,s);
>> text(0.5,0,'\fontsize{14}\ity=xsinx')
>>text(2.5,3.5,['\fontsize{14}\its=','{\fontsize{16} \int_{\fontsize{8}0}^{ x}}','\fontsize{14}\itxsinxdx'])

(9)泛函绘图
泛函函数fplot(‘function’,limits,LineSpec)
fplot(‘function’,limits,LineSpec,tol)
说明:
(1)在指定的范围limits内绘制出函数名为function的一元函数图像,其中limits是一个指定x轴的向量[xmin xmax],或者是x轴和y轴的范围向量[xmin xmax ymin ymax]。Tol为相对允许误差,默认值为2e-3.
(2)函数function必须是M函数文件或者只包含一个变量x的函数字符串。
(3)用指定的线型LineSpec绘制出函数function.
For example:
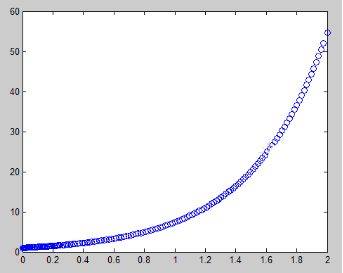
fplot('exp(2*x)',[0 2],'o')
图像为:
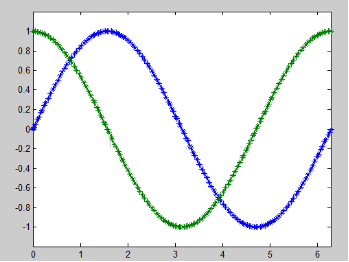
fplot(‘[sin(x),cos(x)]’,[0 2*pi-1.2 1.2],’-*’,1e-3)
(10)简易函数绘图
格式:ezplot(f) %对于显函数f=f(x),在-pi<=x<=pi(默认)上绘制f(x)的图形;对于隐函数f=f(x,y),在[-2pi<=x<=2pi,-2pi<=y<=2pi](默认)上绘制函数f(x,y)的图形。
ezplot(f,[min,max]) %在指定的范围min<=x<=max绘制函数f=f(x)的图形。
ezplot(f,[xmin,xmax],fign) %在指定标号fign的窗口中,指定的范围。[xmin,xmax]内绘制函数f=f(x)的图形。
ezplot(f,[xmin,xmax,ymin,ymax]) %在[xmin<=x<=xmax, ymin<=y<=ymax]绘制f(x,y)=0的图形。
11.matlab 的注释
点击ctrl+R,注释程序;可多次点击,多次注释同一次选中的代码;
点击ctrl+T,取消注释程序。
12.3维图形的绘制
(1)meshgrid
Meshgrid是将向量转换成网络坐标的矩阵函数。
格式:[X,Y]=meshgrid(x,y) %生成二元函数z=f(x,y)在XY平面上的矩阵定义域数据点矩阵X和Y
[X,Y,Z]=meshgrid(x,y,z) %生成三元函数u=f(x,y,z)中立方体定义域中的数据点矩阵X,Y,Z.
(2) plot3
%X,Y,Z为同维向量组,分别表示曲线上点集的横坐标,纵坐标,和函数值。
plot3(X,Y,Z,LineSpec) %LineSpec表线性、标记符号、和颜色的字符串。
说明:常用来绘制单变量的参数曲线x=x(t),y=y(t)与z=z(t)的三维函数图形。
(3)mesh 画网格曲面
mesh(X,Y,Z,C) %X,Y为坐标轴取值向量,Z为X,Y平面上的函数值矩阵,C为色彩向量,当C固定时,网格图的色彩随Z的高度而改变。
例如:
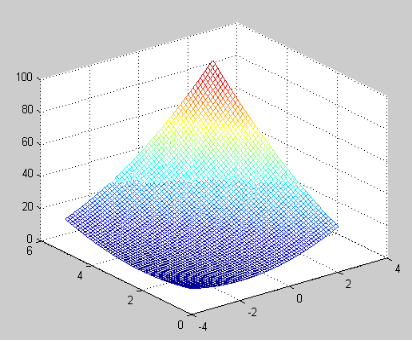
x=-3:0.1:3;y=1:0.1:6;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
mesh(X,Y,Z)
(4)表面图 surf
格式:surf(X,Y,Z) %X,Y,Z为同维向量组,分别表示曲线上点集的横坐标、纵坐标和函数值,绘制出数据点(X,Y,Z)表示的曲面。
例如:
t=linspace(0,pi/2,25);p=linspace(0,pi/2,25);
[theta,phi]=meshgrid(t,p);
x=cos(theta).*cos(phi);y=cos(theta).*sin(phi);z=sin(theta);
surf(x,y,z);
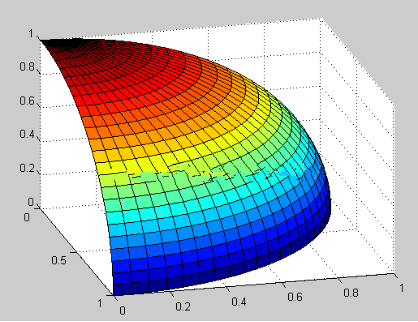
(5)set函数
set函数就是给一些图像设置属性的。
1.MATLAB给每种对象的每一个属性规定了一个名字,称为属性名,而属性名的取值成为属性值。例如,LineStyle是曲线对象的一个属性名,它的值决定着线型,取值可以是'-'、':'、'-.'、'--'或'none'。
2.属性的操作
set函数的调用格式为:
set(句柄,属性名1,属性值1,属性名2,属性值2,…)
[fia,theta]=meshgrid([linspace(0,pi/2,5),pi/2])
x=cos(theta).*cos(fia);
y=cos(theta).*sin(fia);
z=sin(theta);
shading interp
% mesh(x,y,z)
set(mesh(x,y,z),'FaceColor','k','EdgeColor','none');
shading interp;
alpha(0.2);
hold on
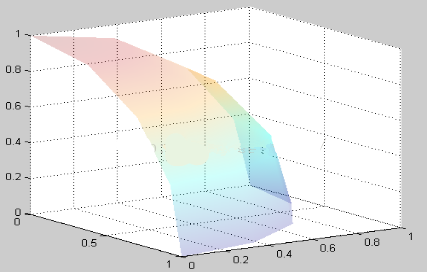
(6)alpha函数
alpha函数就是控制色彩的浓稠度的,
如:alpha(0.5) 色彩的浓稠度就减少了一半。默认情况下是1.
matlab画图基本教程
1.在命令窗口输入命令时,可以不必每输入一条命令就按enter键执行,可以在输入几行后一同运行。方法是:换行时,只要在按住
2.如何将数据文件导入matlab中并画图:点击file中import data,然后就可以导入文件,然后再workspace里面,点击该数据文件,就可以出现以下图形:

选择该两列,就可以看到在上面有一个scatter然后点击,就可以出现以下图形:

3.分号“;”的作用:用做矩阵(数组)的行间分隔符,用做不显示计算结果的命令。
4.稀疏矩阵
定义:矩阵大部分元素是0,少部分元素是非零元素,这种矩阵是稀疏矩阵。
S=sparse(A);
full(S);
nnz(S);
spy(S);


spy(s,,‘*’,16) 表示用’*’号显示,大小为16。如图:

5.注意矩阵的乘法A*B和A.*B的区别:A*B就是A与B的直接相乘,如果是A.*B就是A与B中的对应项相乘。 “./”也是一样的,就是对应项相除。
6.奇异矩阵就是方阵并且行列式为0的矩阵。
7.二维图像绘制
(1)基本函数绘制 ?plot 既可以绘制实线,也可以绘制点线。
<1> plot(X,Y) ?%X,Y为同维向量时,绘制以X、Y元素为横,纵坐标的一条线;X为列向量,Y为矩阵时,按Y列绘制多条不同颜色的曲线,X为这些曲线共同的横坐标。
<2> plot(X,Y,LineSpec) %参数LineSpec用于指出线条的类型,标记符号和颜色。
<3> plot(X1,Y1,LineSpec1,X2,Y2,LineSpec2...) %当Xi和Yi成对出现时,将分别按顺序取两数据Xi和Yi进行画图。
<4> plot(..., ‘PropertyName’,PropertyValue,...)%对图形对象中指定的属性进行设置。
For example:
??x=0:0.1:2;
??y=1+exp(x);
??Plot(x,y, ‘-+b’)

其中,‘-’表示实线,‘+’表示点类型,b表示蓝色。
t=[-pi:pi/100:2*pi]’;k=1:6; y=sin(t)*k;
Plot(t,y) ??%y是矩阵形式

(2)图形标注
<1> 坐标轴名
格式:xlabel(‘string’)
Ylabel(‘string’)
分别给x轴和y轴添加标签
<2> 图名
格式:title(‘string’) 在当前坐标轴上方正中央放置字符串string做为标题。
<3> 图例
格式:legend(‘string1’,’string2’,...)
用指定文字给当前坐标轴添加图例。
For example:
t=0:pi/100:pi;
y1=sin(t);y2=sin(-t);
y3=sin(t).*sin(5*t);
plot(t,y1, ‘-.r’,t,y2, ‘-.k’,t,y3, ‘-bo’)
xlabel(‘时间’);ylabel(‘幅度’);
Title(‘波形及包络线’);
Legend(‘y=sint’, ‘y=-sint’, ‘y=sinsin5t’)

上面的图形标注都是使用标注函数直接写在程序中的,当执行程序后,图形中会自动添加图形标注。但是我们也可以根据图形菜单进行标注,打开图形窗口(Figure)菜单栏中的insert菜单,这时候就可以在图像上添加标注。
(3)图像控制命令
<1>clf %清除所有当前图像窗口
(4)迭加绘图
<1>hold on%保留当前图像与当前坐标轴的属性值,使用后面的图形命令只能在当前存在的坐标轴中增加图形。
<2>hold off %在绘制新图形之前,重新设置坐标轴的属性为默认值,关闭hold on功能。
<3>hold%在on和off之间切换,即在增加图形和覆盖图形之间切换。
<4>hold all %保留当前颜色和线型,在绘制随后的图形时使用当前颜色和线型。
For example:
x=linspace(0,2*pi,60);y=sin(x);
plot(x,y,’b’);
xlabel(‘自变量’),ylabel(‘因变量’);
Hold on;
z=0.5*sin(x);
plot(x,z,’k:’);
legend(‘y=sin(x)’,’z=0.5*sin(x)’);
hold off

(5)多子图
在同一图形框内布置几幅独立的子图。
格式:subplot(m,n,k) %将一个图形窗口分成m*n个小窗口(子图),k是子图的编号。序号原则是:左上方的为第一幅,然后向右、向下依次排好。
subplot(‘Position’,[left bottom width height]) %在由4个元素指定的位置上创建坐标轴。
x=-4:0.1:4;
subplot(2,2,1);
y1=1/sqrt(2*pi)*exp(-1/2*x.^2),plot(x,y1);
xlabel('变量x'),ylabel('变量密度y'),title('正太分布N(0,1)');
subplot(2,2,2);
y2=1/sqrt(2*pi)/2*exp(-1/2/4*x.^2),plot(x,y2);
xlabel('变量x'),ylabel('概率密度y')
title('正太分布N(0,4)');
subplot(2,2,3);
y3=1/sqrt(2*pi)/0.5*exp(-1/2/(0.5^2)*(x-1).^2),plot(x,y3);
xlabel('变量x'),ylabel('概率密度y'),title('正太分布N(1,1/4)');
subplot(2,2,4);
y4=1/sqrt(2*pi)/0.5*exp(-1/2/(0.5^2)*(x+1).^2),plot(x,y4)
xlabel('变量x'),ylabel('概率密度y'),title('正太分布N(-1,1/4)')

(6)多个图形窗口
格式: Figure(n) %创建新的图形窗口或显示当前图形窗口。n是这个窗口的编号,figure(1)是默认值,不需要声明。
>> t=-4:0.1:4;x=sin(t);plot(t,x,'b^')
>> t=-4:0.1:4;x=sin(t);plot(t,x,'b^')
>> xlabel('t');ylabel('x');title('函数x=sint的图形');
>> figure(2)
>> y=cos(t);plot(t,y,'kp');
>> xlabel('t');ylabel('y');title('函数y=cost的图形');
>> figure(3)
>> z=sin(t).*cos(t);plot(t,z,'kh')
>> xlabel('t');ylabel('z');title('函数z=sincost的图形')

(7)对数比例坐标轴
loglog(x,y) %双对数坐标,在x轴,y轴按对数比例绘制二维图形。
Semilogx %半对数坐标,在x轴按对数比例,y轴按线型比例绘制二维图形。
Semilogy %半对数坐标,在y轴按对数比例,x轴按线型比例绘制二维图形。
x=linspace(0,5,20);y=exp(x);
>> subplot(2,2,1),plot(x,y),xlabel('x'),ylabel('y');
>> subplot(2,2,2),loglog(x,y),xlabel('logx'),ylabel('logy');
>> subplot(2,2,3),semilogx(x,y),xlabel('logx'),ylabel('y');
>> subplot(2,2,4),semilogy(x,y),xlabel('x'),ylabel('logy');
>>

(8)双纵坐标图
格式:plotyy(x1,y1,x2,y2) %绘制双纵坐标二维图形,x1和y1所对应的图形的纵坐标标注在图形的左边,x2和y2所对应图形的纵坐标标注在图形的右边。
>> x=0:0.1:4;y=x.*sin(x);s=sin(x)-x.*cos(x);
>> plotyy(x,y,x,s);
>> text(0.5,0,'\fontsize{14}\ity=xsinx')
>>text(2.5,3.5,['\fontsize{14}\its=','{\fontsize{16} \int_{\fontsize{8}0}^{ x}}','\fontsize{14}\itxsinxdx'])

(9)泛函绘图
泛函函数fplot(‘function’,limits,LineSpec)
fplot(‘function’,limits,LineSpec,tol)
说明:
(1)在指定的范围limits内绘制出函数名为function的一元函数图像,其中limits是一个指定x轴的向量[xmin xmax],或者是x轴和y轴的范围向量[xmin xmax ymin ymax]。Tol为相对允许误差,默认值为2e-3.
(2)函数function必须是M函数文件或者只包含一个变量x的函数字符串。
(3)用指定的线型LineSpec绘制出函数function.
For example:
fplot('exp(2*x)',[0 2],'o')
图像为:

fplot(‘[sin(x),cos(x)]’,[0 2*pi-1.2 1.2],’-*’,1e-3)

(10)简易函数绘图
格式:ezplot(f) %对于显函数f=f(x),在-pi<=x<=pi(默认)上绘制f(x)的图形;对于隐函数f=f(x,y),在[-2pi<=x<=2pi,-2pi<=y<=2pi](默认)上绘制函数f(x,y)的图形。
ezplot(f,[min,max]) %在指定的范围min<=x<=max绘制函数f=f(x)的图形。
ezplot(f,[xmin,xmax],fign) %在指定标号fign的窗口中,指定的范围。[xmin,xmax]内绘制函数f=f(x)的图形。
ezplot(f,[xmin,xmax,ymin,ymax]) %在[xmin<=x<=xmax, ymin<=y<=ymax]绘制f(x,y)=0的图形。
11.matlab 的注释
点击ctrl+R,注释程序;可多次点击,多次注释同一次选中的代码;
点击ctrl+T,取消注释程序。
12.3维图形的绘制
(1)meshgrid
Meshgrid是将向量转换成网络坐标的矩阵函数。
格式:[X,Y]=meshgrid(x,y) %生成二元函数z=f(x,y)在XY平面上的矩阵定义域数据点矩阵X和Y
[X,Y,Z]=meshgrid(x,y,z) %生成三元函数u=f(x,y,z)中立方体定义域中的数据点矩阵X,Y,Z.
(2) plot3
%X,Y,Z为同维向量组,分别表示曲线上点集的横坐标,纵坐标,和函数值。
plot3(X,Y,Z,LineSpec) %LineSpec表线性、标记符号、和颜色的字符串。
说明:常用来绘制单变量的参数曲线x=x(t),y=y(t)与z=z(t)的三维函数图形。
(3)mesh 画网格曲面
mesh(X,Y,Z,C) %X,Y为坐标轴取值向量,Z为X,Y平面上的函数值矩阵,C为色彩向量,当C固定时,网格图的色彩随Z的高度而改变。
例如:
x=-3:0.1:3;y=1:0.1:6;
[X,Y]=meshgrid(x,y);
Z=(X+Y).^2;
mesh(X,Y,Z)

(4)表面图 surf
格式:surf(X,Y,Z) %X,Y,Z为同维向量组,分别表示曲线上点集的横坐标、纵坐标和函数值,绘制出数据点(X,Y,Z)表示的曲面。
例如:
t=linspace(0,pi/2,25);p=linspace(0,pi/2,25);
[theta,phi]=meshgrid(t,p);
x=cos(theta).*cos(phi);y=cos(theta).*sin(phi);z=sin(theta);
surf(x,y,z);

(5)set函数
set函数就是给一些图像设置属性的。
1.MATLAB给每种对象的每一个属性规定了一个名字,称为属性名,而属性名的取值成为属性值。例如,LineStyle是曲线对象的一个属性名,它的值决定着线型,取值可以是'-'、':'、'-.'、'--'或'none'。
2.属性的操作
set函数的调用格式为:
set(句柄,属性名1,属性值1,属性名2,属性值2,…)
[fia,theta]=meshgrid([linspace(0,pi/2,5),pi/2])
x=cos(theta).*cos(fia);
y=cos(theta).*sin(fia);
z=sin(theta);
shading interp
% mesh(x,y,z)
set(mesh(x,y,z),'FaceColor','k','EdgeColor','none');
shading interp;
alpha(0.2);
hold on

(6)alpha函数
alpha函数就是控制色彩的浓稠度的,
如:alpha(0.5) 色彩的浓稠度就减少了一半。默认情况下是1.
常用指令介绍
单位矩阵创建
在线性代数运算时,常需要单位矩阵E,在matlab中可使用eyes函数,如下所示即为其语法:
Y = eye(n)
Y = eye(m,n)
Y = eye([m n])
Y = eye(size(A))
Y = eye
Y = eye(m, n, classname)
作为示例,常用Y = eye(n)指令,比如要3x3单位矩阵,则可以如下指令:
>> Y = eye(3)
输出:
Y =
1 0 0
0 1 0
0 0 1

·全零矩阵
在线性代数运算时,有时候需要全零矩阵,可使用zeros函数。
B = zeros(n)
B = zeros(m,n)
B = zeros([m n])
B = zeros(m,n,p,...)
B = zeros([m n p ...])
B = zeros(size(A))
Y = zeros
zeros(m, n,...,classname)
zeros([m,n,...],classname)
以上是其全部语法,常用的指令是:B = zeros(n)与 B = zeros(m,n)如下:
>> B = zeros(3)
输出:
B =
0 0 0
0 0 0
0 0 0

·元素全为1阵
在矩阵运算时,会遇到元素全为1矩阵,此时可以借助于ones函数。
Y = ones(n)
Y = ones(m,n)
Y = ones([m n])
Y = ones(m,n,p,...)
Y = ones([m n p ...])
Y = ones(size(A))
Y = ones
ones(m, n,...,classname)
ones([m,n,...],classname)
如上是其全部语法,其中常用的还是:Y = ones(n) 与 Y = ones(m,n) 如下示例:
>> Y = ones(3)
输出:
Y =
1 1 1
1 1 1
1 1 1
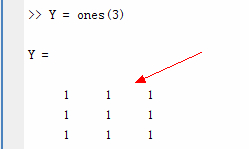
Matlab画散点图教程单位矩阵创建
在线性代数运算时,常需要单位矩阵E,在matlab中可使用eyes函数,如下所示即为其语法:
Y = eye(n)
Y = eye(m,n)
Y = eye([m n])
Y = eye(size(A))
Y = eye
Y = eye(m, n, classname)
作为示例,常用Y = eye(n)指令,比如要3x3单位矩阵,则可以如下指令:
>> Y = eye(3)
输出:
Y =
1 0 0
0 1 0
0 0 1

·全零矩阵
在线性代数运算时,有时候需要全零矩阵,可使用zeros函数。
B = zeros(n)
B = zeros(m,n)
B = zeros([m n])
B = zeros(m,n,p,...)
B = zeros([m n p ...])
B = zeros(size(A))
Y = zeros
zeros(m, n,...,classname)
zeros([m,n,...],classname)
以上是其全部语法,常用的指令是:B = zeros(n)与 B = zeros(m,n)如下:
>> B = zeros(3)
输出:
B =
0 0 0
0 0 0
0 0 0

·元素全为1阵
在矩阵运算时,会遇到元素全为1矩阵,此时可以借助于ones函数。
Y = ones(n)
Y = ones(m,n)
Y = ones([m n])
Y = ones(m,n,p,...)
Y = ones([m n p ...])
Y = ones(size(A))
Y = ones
ones(m, n,...,classname)
ones([m,n,...],classname)
如上是其全部语法,其中常用的还是:Y = ones(n) 与 Y = ones(m,n) 如下示例:
>> Y = ones(3)
输出:
Y =
1 1 1
1 1 1
1 1 1
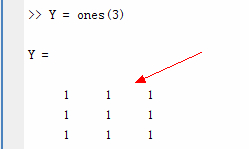
既然要画散点图,自然就需要一些离散的数据了,下面我们就利用matlab生成这些数据,实际应用中我们获得的数据是从其他方式获得的。具体的指令和结果如下图所示:

首先需要先画出点图,即把每一个数据点的位置画出来,所使用的指令为:scatter(x,y1,'k'),该指令主要用于绘制点图,后面''里面的k标示的是每一个点用黑色画出,里面也可以一起添加一些其他的参数:如下图所示:

下面是利用第一步生成的数据和第二步的指令画出的点图,如下图所示,绿色的是y1的数据,红色的是y2的数据。

下面就把点串起来,就大功告成了,使用的指令是:plotyy(x,y1,x,y2,'plot');具体的图形如下图所示:

matlab中关于画图函数plot()的简析
plot() 函数是绘制二维图形的最基本函数,它是针对向量或矩阵的列来绘制曲线的。使用plot 函数之前,必须首先定义好曲线上每一点的x 及y 坐标.下面简单介绍!
plot(x) 当x 为一向量时,以x 元素的值为纵坐标,x 的序号为横坐标值绘制曲线。当x 为一实矩阵时,则以其序号为横坐标,按列绘制每列元素值相对于其序号的曲线
例如:此处用
x=0:pi/20:2*pi;
y1=sin(x);
plot(x,y1);

1, plot(x,y) 以x 元素为横坐标值,y 元素为纵坐标值绘制曲线。
2, plot(x,y1,x,y2,…) 以公共的x 元素为横坐标值,以y1,y2,… 元素为纵坐标值绘制多条曲线。
x=0:pi/20:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,x,y2);

可以在画的图像中添加栅格,用命令grid on,这样可以方便你对齐某条线或是对比比较方便,看下图可以上图对比,看下有什么不同,测试代码如下:
x=0:pi/20:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,x,y2);
grid on

添加坐标轴信息,这样做可以很快的让人明白你在做什么,测试代码如下
x=0:pi/20:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,x,y2);
grid on
xlabel('变量 X')
ylabel('变量 Y1 & Y2')

除了坐标轴信息外还可以添加其它的信息,如所画曲线的信息等:测试代码如下
x=0:pi/20:2*pi;
y1=sin(x);
y2=cos(x);
plot(x,y1,x,y2);
grid on
xlabel('变量 X')
ylabel('变量 Y1 & Y2')
title('正弦余弦波形') %添加图像标题
text(1.5,0.3,'cos(x)') %将cosx这个注解加到坐标中的某个位置
gtext('sin(x)') % 用鼠标的光标定位,将sinx这个注解放在你鼠标点击的地方
通过各图的对比,你就会发现这些命令的用法


【matlab plot画图命令】
1,颜色和线条:b blue 蓝 . point - solid
g green 绿 o circle : dotted
r red 红 x x-mark -. dashdot
c cyan 青 + plus -- dashed
m magenta 品红 * star (none) no line
y yellow 黄 s square
k black 黑 d diamond
w white 白 v triangle (down)
^ triangle (up)
< triangle (left)
> triangle (right)
p pentagram 五角星
h hexagram 六角星
2,plot(x,y):创建2维直线图。例如(以下代码都是在command窗口敲的):
>> x = 0:pi/100:2*pi;
>> y = sin(x);
>> plot(x,y)
图示:

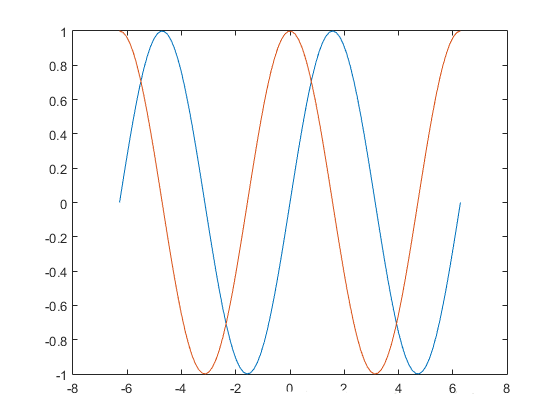
3,plot(X1,Y1,...,Xn,Yn):画n条线。例如:
>> x = linspace(-2*pi,2*pi);
>> y1 = sin(x);
>> y2 = cos(x);
>> plot(x,y1,x,y2)
图示:

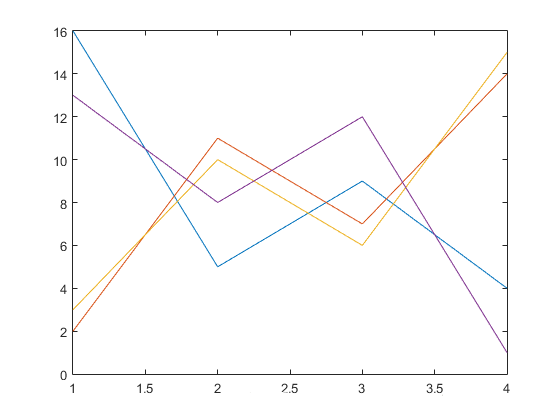
4,plot(Y):Y是矩阵,这表示矩阵的每一行都画一条线。例如:
>> Y = magic(4); % 这是一个4*4的矩阵,详情请在command窗口输入help magic查看
>> plot(Y)
图示:

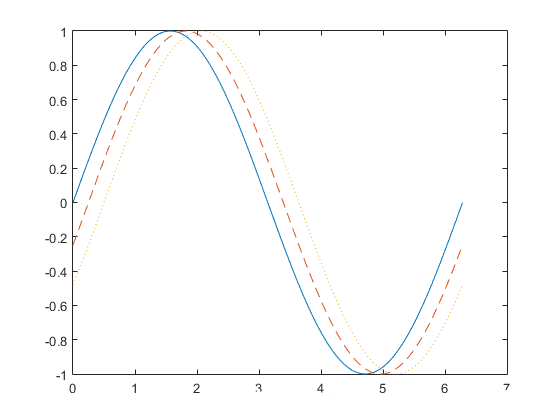
5,plot(x,y1, x,y2,'--', x,y3,':'):画三条不同风格的线,‘’中的内容可以改为第1小节的其他线条。例子如下:
>> x = 0:pi/100:2*pi;
>> y1 = sin(x);
>> y2 = sin(x-0.25);
>> y3 = sin(x-0.5);
>> plot(x,y1,x,y2,'--',x,y3,':')
图示:

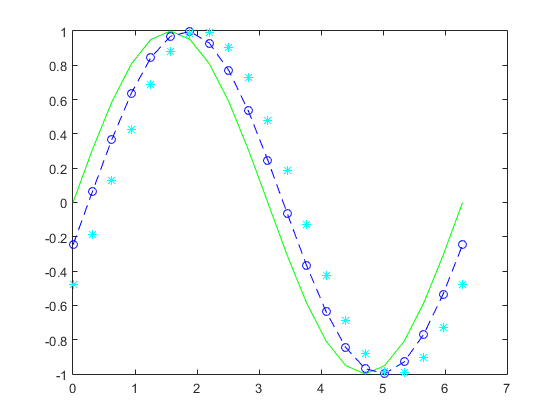
6,plot(x,y1,'g',x,y2,'b--o',x,y3,'c*'):特殊的线条和颜色组合,引号内的就是颜色和线条,可以由第1小节的颜色和线条自由组合。例如:
>> x = 0:pi/10:2*pi;
>> y1 = sin(x);
>> y2 = sin(x-0.25);
>> y3 = sin(x-0.5);
>> plot(x,y1,'g',x,y2,'b--o',x,y3,'c*')
图示:

7,线宽调整
plot(x,y,'--gs','LineWidth',2,'MarkerSize',10,'MarkerEdgeColor','b','MarkerFaceColor',[0.5,0.5,0.5])
这里'--gs'表示用方框画点,然后用绿色虚线连结;'LineWidth',2表示绿色虚线宽度为2;'MarkerSize',10表示方框大小为10;'MarkerEdgeColor','b'表示方框边缘颜色为蓝色;'MarkerFaceColor',[0.5,0.5,0.5]表示方框填充色为[0.5,0.5,0.5](这是RGB颜色值)。例如:
>> x = -pi:pi/10:pi;
>> y = tan(sin(x)) - sin(tan(x));
>> plot(x,y,'--gs','LineWidth',2,'MarkerSize',10,'MarkerEdgeColor','b','MarkerFaceColor',[0.5,0.5,0.5])
图示:

8,标题和坐标轴标签,例如:
>> x = linspace(0,10,150);
>> y = cos(5*x);
>> plot(x,y,'--g')
>> title('2-D Line Plot')
>> xlabel('x')
>> ylabel('cos(5x)')
图示:

9,绘制子图,点这里有详细的讲解。这里还是举个例子:
>> ax1 = subplot(2,1,1); % top subplot
>> ax2 = subplot(2,1,2); % bottom subplo
图示:

10,画圆。例子:
r = 2; % 半径
xc = 4; % (xc,yc)是圆心坐标
yc = 3;
theta = linspace(0,2*pi);
x = r*cos(theta) + xc;
y = r*sin(theta) + yc;
plot(x,y)
axis equal % 把x,y轴设为等距,以便于更好地显示圆。
图示:

【matlab解方程】
如何利用matlab求解方程?1.前言
求解方程是工科学习和工程计算中最基础、最常见的问题。掌握利用现代化工具求解方程的方法对于提升我们的工科素养至关重要。为此,本篇将对matlab中求解方程的方法进行介绍。
2.用法

2.1 指明变量
告诉电脑方程中所含有的变量,包括参数和未知变量。比如:所求解的方程为:,很显然该方程中有a,b,c,x符号变量,因此该步骤的写法为:
syms a b c x
2.2 指明方程,未知数和限制条件(非必需)

2.3 获得所求方程的解
如果为多个函数,该解存储形式为结构体。
3.具体实例
3.1求解sin(x)=1的通解
具体代码:
syms x
[x,params,conds]=solve(sin(x)==1,'ReturnConditions', true)
结果
solx =pi/2+2*pi*k
params =k
conds =in(k,'integer')
可以看出,该方程的通解为:

3.2求解以下方程:
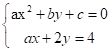
代码:
syms a b c y x
[x,y]=solve([a*x^2+b*y+c==0,a*x+2*y==4],[x,y])
结果:
x =
((a*b)/4-(-(a*(- a*b^2+32*b +16*c))/16)^(1/2))/a
((a*b)/4+(-(a*(- a*b^2+32*b +16*c))/16)^(1/2))/a
y =
(-(a*(- a*b^2+32*b +16*c))/16)^(1/2)/2-(a*b)/8+2
2-(-(a*(- a*b^2+32*b +16*c))/16)^(1/2)/2-(a*b)/8
即:
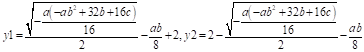
1.解方程、方程组
x^2-4=12,求x:
syms x;
f=x^2-4-12;
solve(f)
最近有多人问如何用matlab解方程组的问题,其实在matlab中解方程组还是很方便的,例如,对于代数方程组Ax=b(A为系数矩阵,非奇异)的求解,MATLAB中有两种方法:
(1)x=inv(A)*b — 采用求逆运算解方程组;
(2)x=A\B — 采用左除运算解方程组
PS:使用左除的运算效率要比求逆矩阵的效率高很多~
例:
x1+2x2=8
2x1+3x2=13
>>A=[1,2;2,3];b=[8;13];
>>x=inv(A)*b
x =
2.00
3.00
>>x=A\B
x =
2.00
3.00;
即二元一次方程组的解x1和x2分别是2和3。
对于同学问到的用matlab解多次的方程组,有符号解法,方法是:先解出符号解,然后用vpa(F,n)求出n位有效数字的数值解.具体步骤如下:
第一步:定义变量syms x y z ...;
第二步:求解[x,y,z,...]=solve('eqn1','eqn2',...,'eqnN','var1','var2',...'varN');
第三步:求出n位有效数字的数值解x=vpa(x,n);y=vpa(y,n);z=vpa(z,n);...。
如:解二(多)元二(高)次方程组:
x^2+3*y+1=0
y^2+4*x+1=0
解法如下:
>>syms x y;
>>[x,y]=solve('x^2+3*y+1=0','y^2+4*x+1=0');
>>x=vpa(x,4);
>>y=vpa(y,4);
结果是:
x =
1.635+3.029*i
1.635-3.029*i
-.283
-2.987
y =
1.834-3.301*i
1.834+3.301*i
-.3600
-3.307。
二元二次方程组,共4个实数根;
还有的同学问,如何用matlab解高次方程组(非符号方程组)?举个例子好吗?
解答如下:
基本方法是:solve(s1,s2,…,sn,v1,v2,…,vn),即求表达式s1,s2,…,sn组成的方程组,求解变量分别v1,v2,…,vn。
具体例子如下:
x^2 + x*y + y = 3
x^2 - 4*x + 3 = 0
解法:
>> [x,y] = solve('x^2 + x*y + y =3','x^2 - 4*x + 3 = 0')
运行结果为
x =
1 3
y =
1 -3/2
即x等于1和3;y等于1和-1.5
或
>>[x,y] = solve('x^2 + x*y + y =3','x^2 - 4*x + 3= 0','x','y')
x =
1 3
y =
1 -3/2
结果一样,二元二方程都是4个实根。
通过这三个例子可以看出,用matlab解各类方程组都是可以的,方法也有多种,只是用到解方程组的函数,注意正确书写参数就可以了,非常方便。
2、变参数非线性方程组的求解
对于求解非线性方程组一般用fsolve命令就可以了,但是对于方程组中某一系数是变化的,该怎么求呢?
%定义方程组如下,其中k为变量
function F = myfun(x,k)
H=0.32;
Pc0=0.23;W=0.18;
F=[Pc0+H*(1+1.5*(x(1)/W-1)-0.5*(x(1)/W-1)^3)-x(2);
x(1)-k*sqrt(x(2))];
%求解过程
H=0.32;
Pc0=0.23;W=0.18;
x0 = [2*W; Pc0+2*H]; % 取初值
options = optimset('Display','off');
k=0:0.01:1; % 变量取值范围[0 1]
for i=1:1:length(k)
kk=k(i);
x = fsolve(@(x) myfun(x,kk), x0, options);%求解非线性方程组
x1(i)=x(1);
x2(i)=x(2);
end
plot(k,x1,'-b',k,x2,'-r');
xlabel('k')
legend('x1','x2')
3、非线性方程数值求解
matlab里solve如何使用,是否有别的函数可以代替它.
matlab里我解y=9/17*exp(-1/2*t)*17^(1/2)*sin(1/2*17^(1/2)*t)=0这样的方程为什么只得到0这一个解,如何可以的到1/2*17^(1/2)*t=n*(pi)这样一族解??
在matlab里面solve命令主要是用来求解代数方程(即多项式)的解,但是也不是说其它方程一个也不能解,不过求解非代数方程的能力相当有限,通常只能给出很特殊的实数解。(该问题给出的方程就是典型的超越方程,非代数方程)
从计算机的编程实现角度讲,如今的任何算法都无法准确的给出任意非代数方程的所有解,但是我们有很多成熟的算法来实现求解在某点附近的解。matlab也不例外,它也只能给出任意非代数方程在某点附近的解,函数有两个:fzero和fsolve,具体用法请用help或doc命令查询吧。如果还是不行,你还可以将问题转化为非线性最优化问题,求解非线性最优化问题的最优解,可以用的命令有:fminbnd,fminsearch, fmincon等等。
*非线性方程数值求解
*单变量非线性方程求解
在MATLAB中提供了一个fzero函数,可以用来求单变量非线性方程的根。该函数的调用格式为:
z=fzero('fname',x0,tol,trace)
其中fname是待求根的函数文件名,x0为搜索的起点。一个函数可能有多个根,但fzero函数只给出离x0最近的那个根。tol控制结果的相对精度,缺省时取tol=eps,trace?指定迭代信息是否在运算中显示,为1时显示,为0时不显示,缺省时取trace=0。
例 求f(x)=x-10x+2=0在x0=0.5附近的根。
步骤如下:
(1) 建立函数文件funx.m。
function fx=funx(x)
fx=x-10.^x+2;
(2) 调用fzero函数求根。
z=fzero('funx',0.5)
z =
0.3758
**非线性方程组的求解
对于非线性方程组F(X)=0,用fsolve函数求其数值解。fsolve函数的调用格式为:
X=fsolve('fun',X0,option)
其中X为返回的解,fun是用于定义需求解的非线性方程组的函数文件名,X0是求根过程的初值,option为最优化工具箱的选项设定。最优化工具箱提供了20多个选项,用户可以使用optimset命令将它们显示出来。如果想改变其中某个选项,则可以调用optimset()函数来完成。例如,Display选项决定函数调用时中间结果的显示方式,其中‘off’为不显示,‘iter’表示每步都显示,‘final’只显示最终结果。optimset(‘Display’,‘off’)将设定Display选项为‘off’。
例 求下列非线性方程组在(0.5,0.5) 附近的数值解。
(1) 建立函数文件myfun.m。
function q=myfun(p)
x=p(1);
y=p(2);
q(1)=x-0.6*sin(x)-0.3*cos(y);
q(2)=y-0.6*cos(x)+0.3*sin(y);
(2) 在给定的初值x0=0.5,y0=0.5下,调用fsolve函数求方程的根。
x=fsolve('myfun',[0.5,0.5]',optimset('Display','off'))
x =
0.6354
0.3734
将求得的解代回原方程,可以检验结果是否正确,命令如下:
q=myfun(x)
q =
1.0e-009 *
0.2375 0.2957
可见得到了较高精度的结果。
4、fsolve函数解方程
[X,FVAL,EXITFLAG,OUTPUT,JACOB]=FSOLVE(FUN,X0,...) returns the
Jacobian of FUN at X.
Examples
FUN can be specified using @:
x = fsolve(@myfun,[2 3 4],optimset('Display','iter'))
where myfun is a MATLAB function such as:
function F = myfun(x)
F = sin(x);
FUN can also be an anonymous function:
x = fsolve(@(x) sin(3*x),[1 4],optimset('Display','off'))
If FUN is parameterized, you can use anonymous functions to capturethe
problem-dependent parameters. Suppose you want to solve the systemof
nonlinear equations given in the function myfun, which isparameterized
by its second argument c. Here myfun is an M-file function suchas
function F = myfun(x,c)
F = [ 2*x(1) - x(2) - exp(c*x(1))
-x(1) + 2*x(2) - exp(c*x(2))];
To solve the system of equations for a specific value of c, firstassign the
value to c. Then create a one-argument anonymous function thatcaptures
that value of c and calls myfun with two arguments. Finally, passthis anonymous
function to FSOLVE:
c = -1; % define parameter first
x = fsolve(@(x) myfun(x,c),[-5;-5])
【举例解一元方程】
先举一例,解方程“x^2+100*x+99=0”。
在Matlab ”Command Window“中输入如下命令:x=solve(‘x^2+100*x+99=0’,‘x’),见下图。

2、回车后,Matlab就求出了这个一元二次方程的解,见下图。

再举一例,解一元三次方程“x^3+1=0”。
在Matlab ”Command Window”中输入如下命令:x=solve(‘x^3+1=0’,‘x’),见下图。

回车后,Matlab就求出了这个一元三次方程“x^3+1=0”的解,见下图。
Matlab解出来的解有三个,其中有一个实数解,两个虚数解。
我们都知道一元三次方程在复数范围内的解有3个,Matlab的解是对的。
如果我们只要“x^3+1=0”的实数解,我们只要取下面图中的第一个解“-1”。

【举例解二元一次方程】
首先来求一个二元一次方程组。
9x+8y=10 式1
13x+14y=12 式2
我们一般的解法是代入法,或者加减消去法。比较繁琐。
这里我们只需输入如下命令即可求出解:[x,y]=solve(‘9*x+8*y=10’,‘13*x+14*y=12’,‘x’,‘y’)。

回车后,Matlab就求出了这个二元一次方程组的解,见下图。

再来求一个二元非线性方程组
x^2+y^2=10 式1
2x+3y=0 式2
这里我们只需输入如下命令即可求出解:[x,y]=solve(‘x^2+y^2=10’,‘2*x+3*y=0’,‘x’,‘y’)。

x^2+y^2=10 式1
2x+3y=0 式2
其实不少人能看出来,上面的二元非线性方程组的解是一个圆与一条直线的交点坐标,我们的一般解法是先消去y,整理成关于x的一元二次方程,然后求出x值,再求出对应y值。
但这里,我们只用到了上面图片里的的一句命令,就求了这两个交点坐标,见下图。

【Matlab求导】
打开matlab软件;
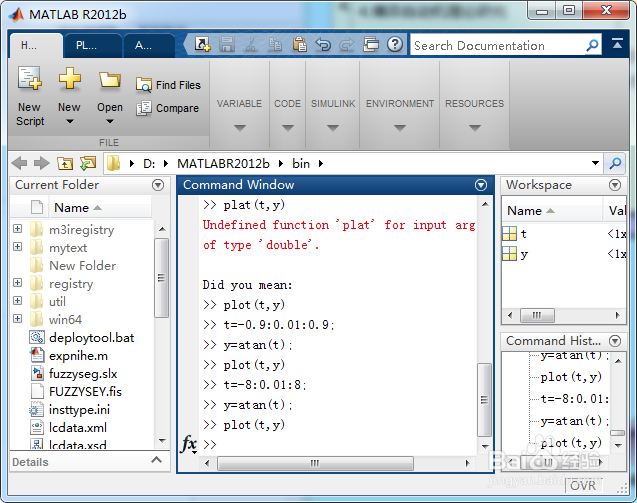
输入一下指令,清空工作空间;
clear;
clc;
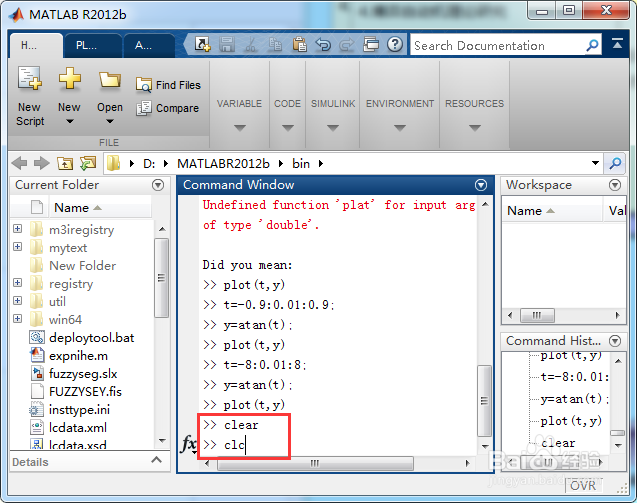
输入一下指令定义一个符号变量,如图所示;
sysm x;
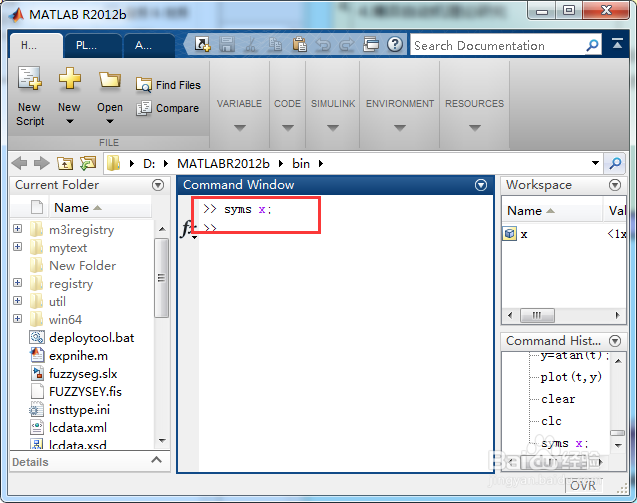
输入一下指令,定义一个函数;
f1=atan(x);
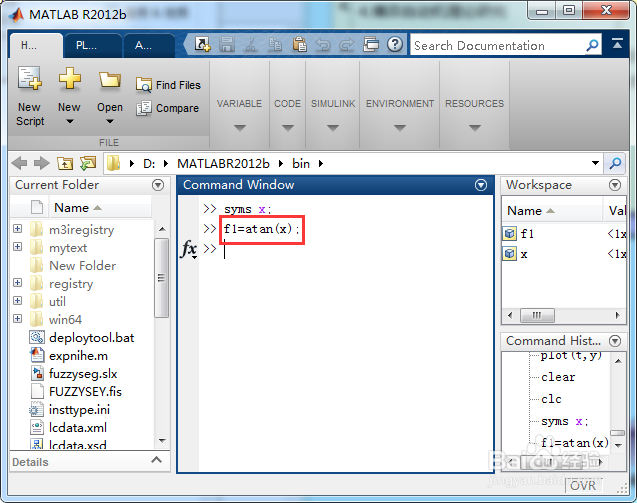
输入一下指令求解导函数的符号解;
df1=diff(f1,x);
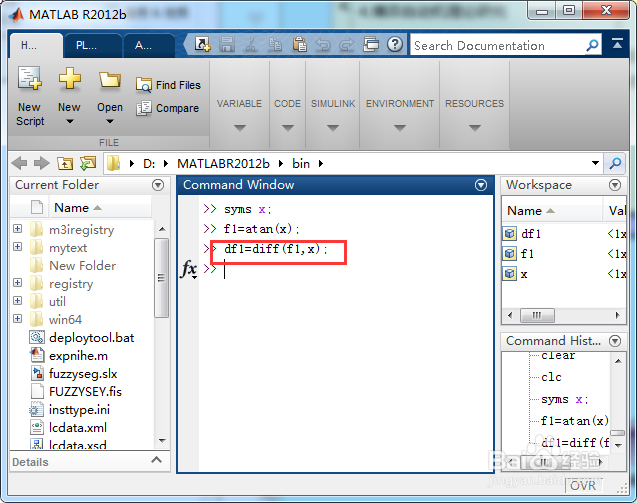
输入一下指令查看求导的结果,如图所示;
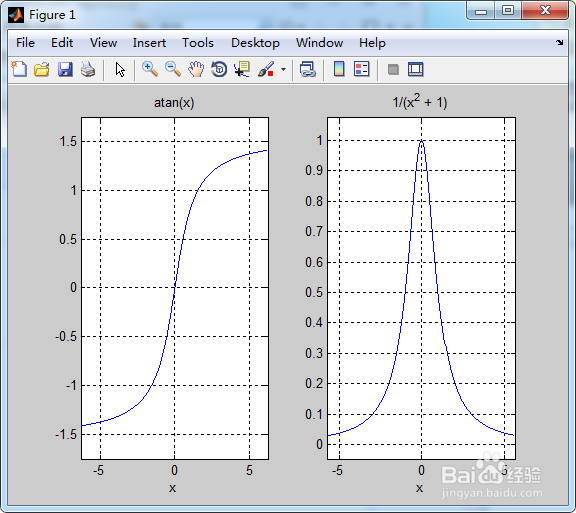
subplot(1,2,1);
ezplot(f1),grid on;
subplot(1,2,2);
ezplot(df1),grid on;
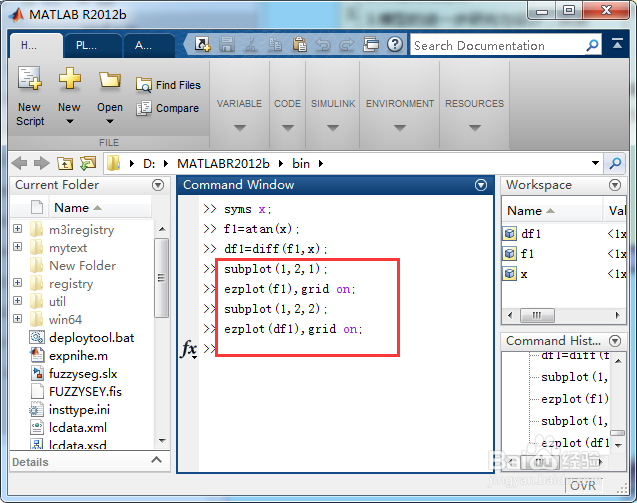
查看求导结果如下。
举例
求一元函数的导数:
输入一下指令,清空工作空间;
clear;
clc;

输入一下指令定义一个符号变量,如图所示;
sysm x;

输入一下指令,定义一个函数;
f1=atan(x);

输入一下指令求解导函数的符号解;
df1=diff(f1,x);

输入一下指令查看求导的结果,如图所示;
subplot(1,2,1);
ezplot(f1),grid on;
subplot(1,2,2);
ezplot(df1),grid on;

查看求导结果如下。

举例
例1:求y=3*sin(x)+4*x^2的导数
syms x;
diff(3*sin(x)+4*x^2)
例2:求y=ln(x+cos(x))
syms x;
diff(log(x+cos(x)))
求一组一元函数的导数:
例3:求f(x)={sin(x)+1;
cos(x)+x;
4*x^4}的导数
syms x;
diff([sin(x)+1,cos(x)+x,4*x^4])
求一元函数的高阶导数:
例4:求y=3*sin(x)+4*x^8的7阶导数
syms x;
diff(3*sin(x)+4*x^8,7)
参数方程形式的函数求导:
例5:已知{x=t^2-ln(2+sint)
{y=t^3-3*sin(ln(t)),求dy/dx。
syms t;
dx_dt=diff(t^2+log(2+sin(t)));
dy_dt=diff(t^3+3*sin(log(t)));
dy_dx=dy_dt/dx_dt
求函数的极值和最值:
例6:计算f(x)在区间[a,b]内的最小值点x和最小值f。
[x,f]=fminbnd('x^2-3*x+1',-10,10)
例7:求函数在某一点附近的局部最小值和最小值点。
[x,f]=fminsearch('sin(2*x)+1',5)
【常见问题】
Matlab7.0出现默认路径等问题怎么解决?经常出现类似这样的问题,一般是路径设置不对,如何设置默认的路径,可以用file-save path

设置路径前,你要先看你现在的文件是哪个路径下,怎么看呢,如下图所示,一个是命令窗口下的文件路径,一个是M文件,也就是函数文件所在目录,如果这个M文件的函数是你自己写的一样要和工程路径放在一起,不然,在调用时就会出错!


出现Undefined function or variable怎么解决?
出现这种问题的原因,一是你的函数调用时写错了,二是你确实使用了未定义或是不存在的函数,三就是上面所的问题,即路径设置不对
还有一个原因,就是函数在保存的时候设置不对,例如下面所示几种函数名都是不对,函数名的保存必须要与你定义的函数名字保持一样或是定义的主函数名一样,函数名不能有“.” 、“-”、或是数字开头,这些字符在函数名中都能导致这种错误

怎么解决fcm错误?
有时直接运行自带函数会出现下面的错误是正常,因为你未正常的调用函数,未赋值给函数所以会出现这样的错误,一旦你正常的调用后,这种错误就会消失


